2017-2018学年数学浙教版九年级下册1.3.2 解直角三角形—利用解直角三角形解实际中的视角问题 同步练习 15
试卷更新日期：2018-04-24 类型：同步测试
一、2017-2018学年数学浙教版九年级下册1.3.2解直角三角形—利用解直角三角形解实际中的视角问题同步练习
-
1. 为解决停车难的问题，在如图所示的一段长56米的路段开辟停车位，每个车位是长5米，宽2.2米的矩形，矩形的边与路的边缘成45°角，那么这个路段最多可以划出个这样的停车位.
2. 如图，从A地到B地的公路需要经过C地，图中AC=10千米，∠CAB=25°，∠CBA=37°.因城市规划的需要，将在A，B两地之间修建一条笔直的公路.
(1)、求改直后的公路AB的长度；(2)、问：公路改造后比原来缩短了多少千米?(sin25°≈0.42，cos25°≈0.91，sin37°≈0.60，tan37°≈0.75)3. 如图，在地面上的点A处测得树顶B的仰角为α度，AC=7米，则树高BC为米.(用含α的代数式表示)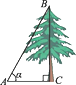
4. 如图所示，热气球探测器在A点处，点B为楼顶，点C为楼底，AD为水平线，EF为经过点A的铅垂线，则下列说法正确的有（ ）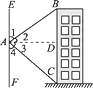
①∠1为仰角； ②∠2为仰角； ③∠3为俯角； ④∠4为俯角.
A、1个 B、2个 C、3个 D、4个5.如图，小敏同学想测量一棵大树的高度．她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°，已知小敏同学身高（AB）为1.6m，则这棵树的高度为（ ）（结果精确到0.1m，≈1.73）．
A、3.5m B、3.6m C、4.3m D、5.1m6. 如图，在数学活动课中，小敏为了测量校园内旗杆AB的高度，站在教学楼上的C处测得旗杆底端B的俯角为45°，测得旗杆顶端A的仰角为30°，若旗杆与教学楼的水平距离CD为9 m，则旗杆的高度是多少?(结果保留根号)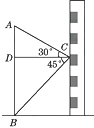
7. 如图，AC是操场上直立的一个旗杆，从旗杆上的B点到地面C涂着红色的油漆，用测角仪测得地面上的D点到B点的仰角是∠BDC=45°，到A点的仰角是∠ADC=60°(测角仪的高度忽略不计).如果BC=3米，那么旗杆的高度AC=米
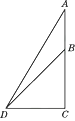8. 如图，在两建筑物之间有一旗杆，高15米，从A点经过旗杆顶点恰好看到矮建筑物的墙脚C点，且俯角α为60°，又从A点测得D点的俯角β为30°，若旗杆底部G为BC的中点，求矮建筑物的高CD.
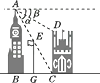9. 如图，热气球的探测器显示，从热气球底部A处看一栋高楼顶部的仰角为30°，看这栋楼底部的俯角为60°，热气球A处与高楼的水平距离为120 m，这栋高楼有多高?( ≈1.732，结果保留一位小数)
10. 如图，某校九年级某班开展数学活动，小明和小军合作用一副三角板测量学校的旗杆，小明站在B点测得旗杆顶端E点的仰角为45°，小军站在点D测得旗杆顶端E点的仰角为30°，已知小明和小军相距(BD)6 m，小明身高(AB)1.5 m，小军身高(CD)1.75 m，求旗杆的高EF.(结果精确到0.1 m，参考数据： ≈1.41， ≈1.73)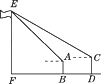
11. 如图，在中俄“海上联合—2014”反潜演习中，我军舰A测得潜艇C的俯角为30°.位于军舰A正上方1 000米的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数)
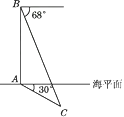12. 如图，某海域有两个海拔均为200米的海岛A和海岛B，一勘测飞机在距离海平面垂直高度为1100米的空中飞行，飞行到点C处时测得正前方一海岛顶端A的俯角是45°，然后沿平行于AB的方向水平飞行1.99×104米到达点D处，在D处测得正前方另一海岛顶端B的俯角是60°，求两海岛间的距离AB.
13. 如图，在电线杆上的C处引拉线CE，CF固定电线杆，拉线CE和地面成60°角，在离电线杆6米的B处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长.(结果保留根号)
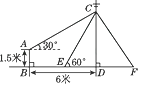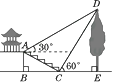
14. 如图，一艘海上巡逻船在A地巡航，这时接到B地海上指挥中心紧急通知：在指挥中心北偏西60°方向的C地有一艘渔船遇险，要求马上前去救援.此时C地位于A地北偏西30°方向上，A地位于B地北偏西75°方向上，A，B两地之间的距离为12海里.求A，C两地之间的距离.(参考数据： ≈1.41， ≈1.73， ≈2.45.结果精确到0.1海里)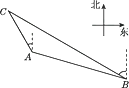
15. 如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°.已知A点的高度AB为3米，台阶AC的坡度为1∶ (即AB∶BC=1∶ )，且B，C，E三点在同一条直线上.请根据以上条件求出树DE的高度.(测倾器的高度忽略不计)