2017-2018学年数学浙教版九年级下册1.3.1 解直角三角形 同步练习
试卷更新日期：2018-04-24 类型：同步测试
一、2017-2018学年数学浙教版九年级下册1.3.1解直角三角形同步练习
-
1. 在Rt△ABC中，∠C=90°，a=4，b=3，则cos A的值是（ ）
A、 B、 C、 D、2. 在△ABC中，∠C=90°，AB=4，AC=3，欲求∠A的值，最适宜的做法是（ ）
A、计算tanA的值求出 B、计算sinA的值求出 C、计算cosA的值求出 D、先根据sinB求出∠B，再利用90°-∠B求出3. 在△ABC中，AB=AC=3，BC=2，则cosB的值是（ ）
A、3 B、 C、3 D、24. 在Rt△ABC中，∠C=90°.(1)、若c=6 ，a=6，则b= ， ∠B= ， ∠A=.(2)、若a=4 ，b=4，则∠A= ， ∠B= ， c=.5. 在Rt△ABC中，∠C=90°.
(1)、若∠B=60°，BC= ，则∠A= ， AC= ， AB=.
(2)、若∠A=45°，AB=2，则∠B= ， AC= ， BC=.
6. 在Rt△ABC中，∠C=90°，∠B=37°，BC=32，则AC=.(参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)
7. 在Rt△ABC中，∠C=90°，AB=12，cos A= ，则AC等于（ ）
A、36 B、 C、4 D、8. 如图是教学用的直角三角板，边AC=30 cm，∠C=90°，tan∠BAC= ，则边BC的长为（ ）
A、30 cm B、20 cm C、10 cm D、5 cm9. 在直角三角形ABC中，已知∠C=90°，∠A=40°，BC=3，则AC等于（ ）
A、3sin40° B、3sin50° C、3tan40° D、3tan50°10. 如图，△ABC中，∠C=90°，AC=3，∠B=30°，P是BC边上的动点，则AP长不可能是（ ）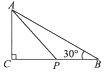
A、3.5 B、4.2 C、5.8 D、711. 如图，在Rt△ABC中，∠C=90°，D为BC上一点，∠DAC=30°，BD=2，AB=2
，则AC的长是（ ）
A、 B、2 C、3 D、12. 如图，在Rt△ABC中，∠C=90°，AC= ，点D为BC边上一点，且BD=2AD，∠ADC=60°，求△ABC的周长.(结果保留根号)
13. 在△ABC中，AB=AC=2，高BE= ，求∠BAC.已知两边解直角三角形的两种类型：
图1 图2
(1)、在Rt△ABC中，已知两直角边a，b，如图1，则c= ，由tanA= 可求∠A，则∠B=90°-∠A.
(2)、在Rt△ABC中，已知斜边和一直角边，如c，a，如图2，则b= ，由sinA= 可求∠A，则∠B=90°-∠A.14. 如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，∠C=45°，sin B= ，AD=1.
(1)、求BC的长；(2)、求tan ∠DAE的值.15. 如图所示，在△ABC中，AB=1，AC= ，sin B= ，求BC的长.
16. 如图，在△ABC中，sin B= ，∠A=105°，AB=2，求△ABC的面积.
17. 如图，在△ABC中，∠BCA=90°，BC=1.5，点F，A，C在同一直线上，∠BAC=30°，DE⊥AB于点D，BE与AB的夹角∠EBD=60°，AD=1，过E点作AC的垂线，交AC的反向延长线于F.求BE及EF的长.
18. 已知钝角三角形ABC，点D在BC的延长线上，连结AD，若∠DAB=90°，∠ACB=2∠D.AD=2，AC= ，根据题意画出示意图，并求tanD的值.
