2017-2018学年数学浙教版九年级下册1.1.2 锐角三角函数—余弦、正切函数 同步练习
试卷更新日期：2018-04-24 类型：同步测试
一、2017-2018学年数学浙教版九年级下册1.1.2锐角三角函数—余弦、正切函数同步练习
-
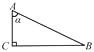
1. 如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，那么cosA的值等于（ ）
A、 B、 C、 D、2. 如图所示，CD是Rt△ABC斜边上的高，AC=4，BC=3，则cos∠BCD的值是（ ）
A、 B、 C、 D、3. 在△ABC中，若三边BC，CA，AB满足BC∶CA∶AB=5∶12∶13，则cosB的值等于（ ）A、 B、 C、 D、4. 在Rt△ABC中，∠C=90°，若sinA= ， 则cosB的值是（ ）A、 B、 C、 D、5. 如图，在Rt△ABC中，∠C=90°，AB=6，cosB= ，则BC的长为.
6. 已知方程x2-4x+3=0的两根为直角三角形的两直角边长,则其最小角的余弦值为.7. 如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，若BD∶CD=3∶2，则tanB=（ ）
A、 B、 C、 D、8. 如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA=（ ）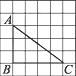
A、 B、 C、 D、9. 如图，已知Rt△ABC中，∠C=90°，AC=4，tanA= ，则BC的长是（ ）
A、2 B、8 C、2 D、410. 在Rt△ABC中，∠C=90°，tanA= ，BC=8，则△ABC的面积为 .
11. 如图，在△ABC中，AB=AC=5，BC=8．若∠BPC= ∠BAC，则tan∠BPC= ．
12. 在Rt△ABC中，∠C=90°，sinA= ，则cosA=.
13. 在Rt△ABC中，∠C=90°，sinA= ，则tanB的值为（ ）A、 B、 C、 D、14. 如图，在直角坐标系中，P是第二象限的点，其坐标是(x，8)，且OP与x轴的负半轴的夹角α的正切值是 ，则x= ， cosα=.
15. 如图，在△ABC中，CD⊥AB，垂足为D.若AB=12，CD=6，tanA= ，求sinB+cosB的值.
16. 在Rt△ABC中，a，b，c分别是∠A，∠B，∠C的对边，∠C=90°，a+b=4，且tanB=1，求c的长.
17. 如图，在4×8的矩形网格中，每个小正方形的边长都为1，△ABC的三个顶点都在格点上，求tan∠BAC的值.
