2017-2018学年数学浙教版八年级下册3.3方差和标准差 同步练习

试卷更新日期：2018-04-23 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 某校A，B两队10名参加篮球比赛的队员的身高（单位：cm）如下表所示：

    1号

    2号

    3号

    4号

    5号

    A队

    176

    175

    174

    171

    174

    B队

    170

    173

    171

    174

    182

    设两队队员身高的平均数分别为 xA¯,xB¯ ，身高的方差分别为SA2 ， SB2 ， 则正确的选项是（   ）

    A、xA¯=xB¯,SA2>SB2 B、xA¯<xB¯,SA2<SB2 C、xA¯>xB¯,SA2>SB2 D、xA¯=xB¯,SA2<SB2

    查看试题解析

  • 2. 在社会实践活动中，某同学对甲、乙、丙、丁四个城市一至五月份的白菜价格进行调查．四个城市5个月白菜的平均值均为3.50元，方差分别为S甲2＝18.3，S乙2＝17.4，S丙2＝20.1，S丁2＝12.5．一至五月份白菜价格最稳定的城市是（   ）


    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 3. 一次数学测试，某小组五名同学的成绩如下表所示（有两个数据被遮盖）．

    组员

    甲

    乙

    丙

    丁

    戊

    方差

    平均成绩

    得分

    81

    79

    ■

    80

    82

    ■

    80

    那么被遮盖的两个数据依次是（    ）

    A、80，2 B、80， 2 C、78，2 D、78， 2

    查看试题解析

  • 4. 下面是甲、乙两人10次射击成绩（环数）的条形统计图，则下列说法正确的是（   ）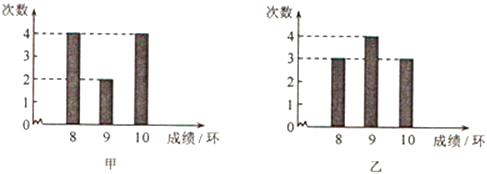

    A、甲比乙的成绩稳定 B、乙比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定谁的成绩更稳定

    查看试题解析

  • 5. 某学习小组5位同学参加初中毕业生实验操作考试（满分20分）的平均成绩是16分．其中三位男生的方差为6（分2），两位女生的成绩分别为17分，15分．则这个学习小组5位同学考试分数的标准差为（     ）
    A、3 B、2 C、6 D、6

    查看试题解析

二、填空题

  • 6. 如果样本方差：S2= 150  [ (x1−5)2  + (x2−5)2  + (x3−5)2  +…+ (x50−5)2 ]，那么这个样本的平均数为 ．

    查看试题解析

  • 7. 对甲、乙、丙三名射击手进行20次测试，平均成绩都是8.5环，方差分别是0.4，3.2，1.6，在这三名射击手中成绩比较稳定的是 ．

    查看试题解析

  • 8. 甲、乙两台机床生产同一种零件，并且每天产量相等，在6天中每天生产零件中的次品数依次是：甲：3、0、0、2、0、1；乙：1、0、2、1、0、2．则甲、乙两台机床中性能较稳定的是 ．

    查看试题解析

  • 9. 已知一组数据5，8，10，x，9的众数是8，那么这组数据的方差是 ．

    查看试题解析

三、解答题

  • 10. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：


    第一次

    第二次

    第三次

    第四次

    第五次

    第六次

    甲

    10

    8

    9

    8

    10

    9

    乙

    10

    7

    10

    10

    9

    8

    (1)、根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；
    (2)、分别计算甲、乙六次测试成绩的方差；
    (3)、根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．

    （计算方差的公式：s2＝ 1n ［ (x1−x¯)2+(x2−x¯)2+⋯+(xn−x¯)2 ］

    查看试题解析

  • 11. 某班实行小组量化考核制，为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到的数据制成如下的统计表：

    (1)、请根据上表中的数据完成下表（注：方差的计算结果精确到0.1）
    (2)、根据综合评价得分统计表中的数据，请在下图中画出乙组综合评价得分的折线统计图．
    (3)、根据折线统计图中的信息，请你分别对甲、乙两个小组连续六周的学习情况作出简要评价．

    查看试题解析

  • 12. 为选派一名学生参加全市实践活动技能竞赛，A、B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试，他俩各加工的10个零件的相关数据依次如下图表所示（单位：mm）

     

     

    平均数

     

    方差

    完全符合

    要求个数

    A

        20

    0.026

        2

      B

        20

      SB2

        5

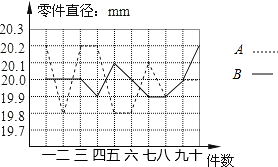
    根据测试得到的有关数据，试解答下列问题：

    (1)、考虑平均数与完全符合要求的个数，你认为谁的成绩好些；
    (2)、计算出SB2的大小，考虑平均数与方差，说明谁的成绩好些；
    (3)、考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由．

    查看试题解析

  • 13. 甲、乙两位同学本学年每个单元的测验成绩如下（单位：分）： 

    甲：98，100，100，90，96，91，89，99，100，100，93

    乙：98，99，96，94，95，92，92，98，96，99，97

    (1)、他们的平均成绩分别是多少？
    (2)、甲、乙的11次单元测验成绩的标准差分别是多少？
    (3)、这两位同学的成绩各有什么特点？
    (4)、现要从中选出一人参加“希望杯”竞赛，历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，你认为应选谁参加这项竞赛，为什么？

    查看试题解析