2017-2018学年数学浙教版八年级下册2.3.2一元二次方程的应用（课时2）同步练习
试卷更新日期：2018-04-23 类型：同步测试
一、选择题
-
1. 如图，将一块正方形空地划出部分区域进行绿化，原空地一边减少了2m，另一边减少了3m，剩余一块面积为20m2的矩形空地，则原正方形空地的边长是（ ）
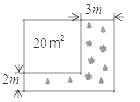A、7m B、8m C、9m D、10m2. 在一幅长80cm、宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图如下图所示，如果要使整个挂图的面积是5 400 cm2 ， 设金色纸边的宽为x cm，那么x满足的方程是（ ）
A、x2＋130x－1 400＝0 B、x2＋65x－350＝0 C、x2－130x－1 400＝0 D、x2－65x－350＝03.如图，在长为100米，宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644米2 ， 则道路的宽应为多少米？设道路的宽为x米，则可列方程为（ ）
A、100×80﹣100x﹣80x=7644 B、（100﹣x）（80﹣x）+x2=7644 C、（100﹣x）（80﹣x）=7644 D、100x+80x=3564. 上海世博会的某纪念品原价168元，连续两次降价a%后售价为128元，下列所列方程中正确的是（ ）
A、168(1＋a%)2＝128 B、168(1－a%)2＝128 C、168(1－2a%)＝128 D、168(1－a2%)＝128二、解答题
-
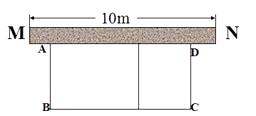
5. 如图S2－1所示，要建一个面积为130 m2的仓库，仓库有一边靠墙(墙长16 m)，并在与墙平行的一边开一道宽1 m的门，现有能围成32 m的木板，求仓库的长与宽？(注意：仓库靠墙的那一边不能超过墙长)．
6. 如图S2－2，在Rt△ABC中，∠C＝90°，AC＝20 cm ， BC＝15 cm.现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB向点B方向运动．如果点P的速度是4 cm/s，点Q的速度是2 cm/s，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动的时间为ts，求：
(1)、用含t的代数式表示Rt△CPQ的面积S；(2)、当t＝3秒时，这时，P、Q两点之间的距离是多少？(3)、当t为多少秒时，S＝S△ABC?
7. 如图，在直角梯形ABCD中，AD∥BC，∠C=90°，BC=16，DC=12，AD=21，动点P从点D出发，沿射线DA的方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，P、Q分别从点D、C同时出发，当点Q运动到点B时，点P随之停止运动，设运动时间为t（s）。
(1)、设△BPQ的面积为S，求S与t之间的函数关系；(2)、当t为何值时，以B、P、Q三点为顶点的三角形是等腰三角形？8. 如图：用同样规格黑白两色的正方形瓷砖铺设矩形地面，请观察下列图形并解答有关问题：
(1)、在第n个图中每一横行共多少块瓷砖，每一竖行共有多少块瓷砖（均用含n的代数式表示）。(2)、设铺设地面所用瓷砖总数为y，请写出y与（1）中n的函数关系式；并求当y=506时，n的值。
(3)、是否存在黑瓷砖与白瓷砖块数相等的情形？请通过计算说明为什么？
9. 利用一面墙（墙的长度不限），另三边用58m长的篱笆围成一个面积为200m2的矩形场地，求矩形的长和宽
