江苏省扬州市邗江区2016-2017学年七年级下学期数学期中考试试卷
试卷更新日期:2018-04-19 类型:期中考试
一、单选题
-
1. 下列计算中正确的是( )A、 B、 C、 D、2. 已知三角形两条边的长分别为2、4,则第三条边的长可以是( )A、1 B、3 C、6 D、73. 下列各式由左边到右边的变形,是因式分解的是( )A、3x(x+y)=3x2+3xy B、-2x2-2xy=-2x(x+y) C、(x+5)(x-5)=x2-25 D、x2+x+1=x(x+1)+14. 已知 ,则A=( )
A、x+y B、﹣x+y C、x﹣y D、﹣x﹣y5. 计算( 4)2017×( )2018的值等于( )
A、 B、4 C、 D、-46. 如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )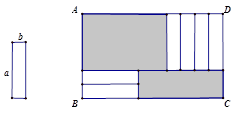 A、140 B、70 C、35 D、247. 已知 能运用完全平方公式分解因式,则 的值为( )
A、140 B、70 C、35 D、247. 已知 能运用完全平方公式分解因式,则 的值为( )
A、12 B、 C、24 D、8. 五张如图1的长为 ,宽为 ( > )的小长方形纸片,按图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则 , 满足( )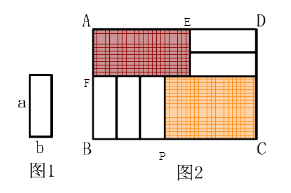 A、 = B、 =2 C、 =3 D、 =4
A、 = B、 =2 C、 =3 D、 =4二、填空题
-
9. DNA分子的直径只有0.000 000 2cm,将0.000 000 2用科学记数法表示为 .10. 若一个多边形的每个外角等于30°,则这个多边形是边形;
11. 已知单项式 与 的积为 ,那么 .
12. 如图,把一个的直角三角尺的直角顶点放在直尺的一边上,已知∠A=30°则∠1+∠2=°.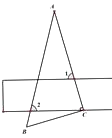 13. 如图,已知DE∥BC,DC平分∠EDB,∠ADE=80°,则∠BCD=°.
13. 如图,已知DE∥BC,DC平分∠EDB,∠ADE=80°,则∠BCD=°.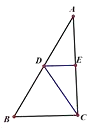 14. 若m=2n+3,则m2﹣4mn+4n2的值是 .15. 若2 +3b=3,则 · 的值为 .
14. 若m=2n+3,则m2﹣4mn+4n2的值是 .15. 若2 +3b=3,则 · 的值为 .
16. 已知 则x= .
17. 如图,AD、BE是△ABC的两条中线,△EDC的面积是2,则△ABD的面积是 .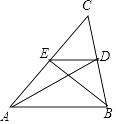 18. 如图,AB∥EF,∠C=60°,∠A=α,∠E=β,∠D=γ,则α、β、γ的关系是 .
18. 如图,AB∥EF,∠C=60°,∠A=α,∠E=β,∠D=γ,则α、β、γ的关系是 .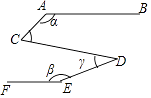
三、解答题
-
19. 计算:
(1)、(2)、(3)、
(4)、20. 因式分解:
(1)、
(2)、(3)、
(4)、9x4-81y421. 已知n为正整数,且x2n=2,求 的值.
22. 先化简,再求值:a (a-3b)+(a +b)2 -a (a-b),其中a=1,b=2.23. 如图,在边长为1个单位长度的小正方形组成的网格中.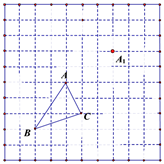 (1)、把△ 平移至 的位置,使点 与 对应,得到△ ;(2)、线段 与 的关系是:;
(1)、把△ 平移至 的位置,使点 与 对应,得到△ ;(2)、线段 与 的关系是:;
(3)、求△ 的面积.24. 如图,BE∥DF,∠B=∠D,求证:AD∥BC. 25. 探索题:图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
25. 探索题:图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
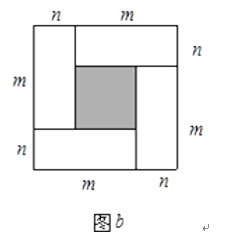 (1)、请用两种不同的方法,求图b中阴影部分的面积:
(1)、请用两种不同的方法,求图b中阴影部分的面积:方法1:; 方法2:;
(2)、观察图b,写出代数式 , , 之间的等量关系,并通过计算验证;
(3)、根据(2)题中的等量关系,解决如下问题:若 , ,求 的值.26. 问题背景:对于形如 这样的二次三项式,可以直接用完全平方公式将它分解成 ,对于二次三项式 ,就不能直接用完全平方公式分解因式了.此时常采用将 加上一项 ,使它与 的和成为一个完全平方式,再减去 ,整个式子的值不变,于是有:=
= = = =
问题解决:
(1)、请你按照上面的方法分解因式: ;(2)、已知一个长方形的面积为 ,长为 ,求这个长方形的宽.27. 【问题探究】如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;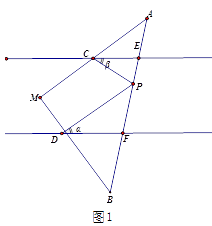
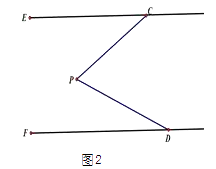
【问题迁移】
如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.
(1)、当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC=°
(2)、如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC与α、β之间的数量关系,并说明理由.
28. 先阅读,再回答问题:要比较代数式A、B的大小,可以作差A-B,比较差的取值,当A-B>0时,有A>B;当A-B=0时,有A=B;当A-B<0时,有A<B.”例如,当a<0时,比较 的大小.可以观察 因为当a<0时,-a>0,所以当a<0时,
(1)、已知M= ,比较M、N的大小关系.
(2)、某种产品的原料提价,因而厂家决定对于产品进行提价,现有三种方案:方案1:第一次提价p%,第二次提价q%;
方案2:第一次提价q%,第二次提价p%;
方案3:第一、二次提价均为
如果设原价为a元,请用含a、p、q的式子表示提价后三种方案的价格.
如果p,q是不相等的正数,三种方案哪种提价最多?