广西桂梧高中2017-2018学年高一上学期数学期末考试试卷
试卷更新日期:2018-04-17 类型:期末考试
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 已知幂函数 的图像经过点 ,则 的值等于( )
A、 B、 C、 D、3. 过点 且垂直于直线 的直线方程为( )A、 B、 C、 D、4. 若不论 取何实数,直线 恒过一定点,则该点的坐标( )A、 B、 C、 D、5. 设l是直线,α,β是两个不同的平面,则下列说法正确的是( )A、若l∥α,l∥β,则α∥β B、若l∥α,l⊥β,则α⊥β C、若α⊥β,l⊥α,则l∥β D、若α⊥β,l∥α,则l⊥β6. 一个几何体的三视图如图所示,则该几何体的侧面积为( )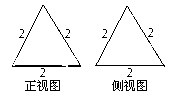
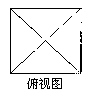 A、 B、 C、 D、7. 直线 与圆 的位置关系( )A、相切 B、相离 C、相交但不过圆心 D、相交且过圆心8. 直线 被圆 截得的弦长为( )A、 B、 C、 D、9. 设实数 满足: , , ,则 的关系( )A、 B、 C、 D、10. 函数 与 图像交点的横坐标所在区间是( )A、 B、 C、 D、11. 已知直线 过定点 ,且与以 , 为端点的线段(包含端点)有交点,则直线 的斜率 的取值范围是( )A、 B、 C、 D、12. 点 在同一个球的球面上, ,若四面体 体积的最大值为 ,则这个球的表面积为( )
A、 B、 C、 D、7. 直线 与圆 的位置关系( )A、相切 B、相离 C、相交但不过圆心 D、相交且过圆心8. 直线 被圆 截得的弦长为( )A、 B、 C、 D、9. 设实数 满足: , , ,则 的关系( )A、 B、 C、 D、10. 函数 与 图像交点的横坐标所在区间是( )A、 B、 C、 D、11. 已知直线 过定点 ,且与以 , 为端点的线段(包含端点)有交点,则直线 的斜率 的取值范围是( )A、 B、 C、 D、12. 点 在同一个球的球面上, ,若四面体 体积的最大值为 ,则这个球的表面积为( )
A、 B、 C、 D、二、填空题
-
13. 计算: .14. 已知直线 与直线 平行,则它们之间的距离
是.
15. 已知在四面体 中, , 分别是 , 的中点,若 , , ,则 与 所成的角的度数为.16. 已知函数 为 上的单调减函数,则实数 的取值范围是 .三、解答题
-
17. 已知直线 经过点 ,其倾斜角为60°.
(1)、求直线 的方程;(2)、求直线 与两坐标轴围成三角形的面积.18. 求圆心为直线 和 的交点, 且与直线 相切的圆的方程.19. 已知关于 , 的方程 : .(1)、若方程 表示圆,求 的取值范围;(2)、若圆 与直线 : 相交于 , 两点,且 ,求 的值.20. 如图,在矩形ABCD中, , 是 的中点,以 为折痕将 向上折起,使 到 点位置,且 .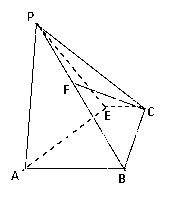
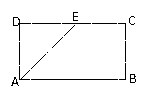
(Ⅰ)若 是 的中点,求证: 面 ;
(Ⅱ)求证:面 面 .