安徽省皖江名校2018届高三12月份大联考理数试卷
试卷更新日期:2018-04-17 类型:高考模拟
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 著名数学家欧拉发规了复数的三角形式: (其中 为虚数单位, ),根据这个公式可知, 表示的复数在复平面中所对应的点位于( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限3. “ ”是方程 有2个实数解得( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 某多面体的三视图如图所示,则该多面体的外接球的表面积是( ) A、 B、 C、 D、5. 已知 中, 的对边分别为 ,若 且 ,则 ( )A、2 B、 C、 D、6. 若某程序框图如图所示,运行后输出 的值是6,则输入的整数 可能的取值是( )
A、 B、 C、 D、5. 已知 中, 的对边分别为 ,若 且 ,则 ( )A、2 B、 C、 D、6. 若某程序框图如图所示,运行后输出 的值是6,则输入的整数 可能的取值是( ) A、16,32 B、5,64 C、5,32 D、5,167. 由直线 及曲线 所围成的封闭图形的面积为( )A、3 B、 C、 D、8. 下列四个命题:
A、16,32 B、5,64 C、5,32 D、5,167. 由直线 及曲线 所围成的封闭图形的面积为( )A、3 B、 C、 D、8. 下列四个命题:; ; ; .
其中的真命题是( )
A、 , B、 , C、 , D、 ,9. 若函数 的图象在区间 上只有一个极值点,则 的取值范围为( )A、 B、 C、 D、10. 在不等式组 所表示的平面区域上,点 在曲线 上,那么 的最小值是( )A、 B、 C、 D、111. 已知正项等比数列 的前 项和为 ,且 ,则 的最小值为( )A、10 B、15 C、20 D、2512. 设函数 在 上存在导函数 ,对任意的实数 都有 ,当 时, .若 ,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 如图甲所示,在直角 中, , 是垂足,则有 ,该结论称为射影定理.如图乙所示,在三棱锥 中, 平面 , 平面 , 为垂足,且 在 内,类比直角三角形中的射影定理,则有 .
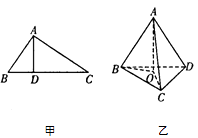 14. 已知函数 ,其中 且 ,若函数 的图象上有且只有一对点关于 轴对称,则 的取值范围是 .15. 已知点 是 的外接圆圆心,且 .若存在非零实数 ,使得 ,且 ,则 .16. 已知数列 , 是其前 项的和且满足 ,则 .
14. 已知函数 ,其中 且 ,若函数 的图象上有且只有一对点关于 轴对称,则 的取值范围是 .15. 已知点 是 的外接圆圆心,且 .若存在非零实数 ,使得 ,且 ,则 .16. 已知数列 , 是其前 项的和且满足 ,则 .
三、解答题
-
17. 在 中.设内角 的对边分别为 ,向量 ,向量 , .(1)、求角 的大小;(2)、若 ,且 ,求 的面积.18. 等差数列 和等比数列 的各项均为正整数,且 的前 项和为 ,数列 是公比为16的等比数列, .(1)、求 ;(2)、求证 .19. 如图 是圆柱体 的母线, 是底面圆的直径, 分别是 的中点, .
 (1)、求证: 平面 ;(2)、求点 到平面 的距离;(3)、求二面角 的大小.
(1)、求证: 平面 ;(2)、求点 到平面 的距离;(3)、求二面角 的大小.
