备考2018年中考数学一轮基础复习:专题二十七 探索规律问题
试卷更新日期:2018-04-16 类型:一轮复习
一、单选题
-
1. 按照一定规律排列的n个数:﹣2、4、﹣8、16、﹣32、64、…,若最后三个数的和为768,则n为( )A、9 B、10 C、11 D、122. 如图,用相同的小正方形按照某种规律进行摆放,则第8个图形中小正方形的个数是( )
 A、71 B、78 C、85 D、893. 将一组数 ,2, ,2 , ,…,2 ,按下列方式进行排列:
A、71 B、78 C、85 D、893. 将一组数 ,2, ,2 , ,…,2 ,按下列方式进行排列:,2, ,2 , ;
2 , ,4,3 ,2 ;
…
若2的位置记为(1,2),2 的位置记为(2,1),则 这个数的位置记为( )
A、(5,4) B、(4,4) C、(4,5) D、(3,5)4.我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 , , ,…得到斐波那契螺旋线,然后顺次连结P1P2 , P2P3 , P3P4 , …得到螺旋折线(如图),已知点P1(0,1),P2(﹣1,0),P3(0,﹣1),则该折线上的点P9的坐标为( )
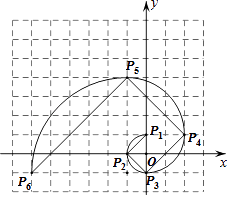 A、(﹣6,24) B、(﹣6,25) C、(﹣5,24) D、(﹣5,25)5. 在公园内,牡丹按正方形种植,在它的周围种植芍药,如图反映了牡丹的列数(n)和芍药的数量规律,那么当n=11时,芍药的数量为( )
A、(﹣6,24) B、(﹣6,25) C、(﹣5,24) D、(﹣5,25)5. 在公园内,牡丹按正方形种植,在它的周围种植芍药,如图反映了牡丹的列数(n)和芍药的数量规律,那么当n=11时,芍药的数量为( ) A、84株 B、88株 C、92株 D、121株6.
A、84株 B、88株 C、92株 D、121株6.如图,过点A0(2,0)作直线l:y= x的垂线,垂足为点A1 , 过点A1作A1A2⊥x轴,垂足为点A2 , 过点A2作A2A3⊥l,垂足为点A3 , …,这样依次下去,得到一组线段:A0A1 , A1A2 , A2A3 , …,则线段A2016A2107的长为( )
 A、( )2015 B、( )2016 C、( )2017 D、( )20187. 观察以下一列数的特点:0,1,﹣4,9,﹣16,25,…,则第11个数是( )A、﹣121 B、﹣100 C、100 D、1218.
A、( )2015 B、( )2016 C、( )2017 D、( )20187. 观察以下一列数的特点:0,1,﹣4,9,﹣16,25,…,则第11个数是( )A、﹣121 B、﹣100 C、100 D、1218.如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
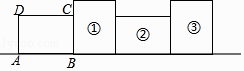 A、2017π B、2034π C、3024π D、3026π9. 如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如
A、2017π B、2034π C、3024π D、3026π9. 如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如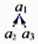 ,表示a1=a2+a3 , 则a1的最小值为( )
,表示a1=a2+a3 , 则a1的最小值为( ) 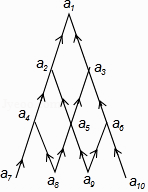 A、32 B、36 C、38 D、4010.
A、32 B、36 C、38 D、4010.如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
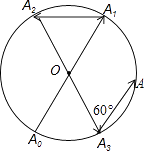 A、4 B、2 C、2 D、011.
A、4 B、2 C、2 D、011.观察下面“品”字形中各数之间的规律,根据观察到的规律得出a的值为( )
 A、23 B、75 C、77 D、13912. 我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
A、23 B、75 C、77 D、13912. 我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A、2017 B、2016 C、191 D、19013.如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1 , 第2幅图形中“●”的个数为a2 , 第3幅图形中“●”的个数为a3 , …,以此类推,则 + + +…+ 的值为( )
 A、 B、 C、 D、14. 观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( )
A、 B、 C、 D、14. 观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( )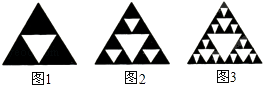 A、121 B、362 C、364 D、72915.
A、121 B、362 C、364 D、72915.填在下面各正方形中四个数之间都有相同的规律,根据这种规律m的值为( )
 A、180 B、182 C、184 D、186
A、180 B、182 C、184 D、186二、填空题
-
16. 在平面直角坐标系中,点P(x,y)经过某种变换后得到点P'(﹣y+1,x+2),我们把点P'(﹣y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2 , 点P2的终结点为P3 , 点P3的终结点为P4 , 这样依次得到P1、P2、P3、P4、…Pn、…,若点P1的坐标为(2,0),则点P2017的坐标为 .17. 某广场用同一种如图所示的地砖拼图案,第一次拼成形如图1所示的图案,第二次拼成形如图2所示的图案,第三次拼成形如图3所示的图案,第四次拼成形如图4所示的图案…按照这样的规律进行下去,第n次拼成的图案共有地砖块.
 18. 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2017的坐标是 .
18. 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2017的坐标是 .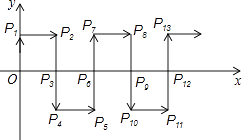 19. 设△ABC的面积为1.
19. 设△ABC的面积为1.如图1,分别将AC,BC边2等分,D1 , E1是其分点,连接AE1 , BD1交于点F1 , 得到四边形CD1F1E1 , 其面积S1= .
如图2,分别将AC,BC边3等分,D1 , D2 , E1 , E2是其分点,连接AE2 , BD2交于点F2 , 得到四边形CD2F2E2 , 其面积S2= ;
如图3,分别将AC,BC边4等分,D1 , D2 , D3 , E1 , E2 , E3是其分点,连接AE3 , BD3交于点F3 , 得到四边形CD3F3E3 , 其面积S3= ;
…
按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形CDnFnEn , 其面积Sn= .
 20.
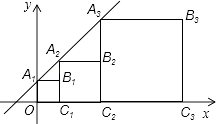
20.正方形A1B1C1O,A2B2C2C1 , A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则An的坐标是 .
 21. 如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2 , 如此继续下去,则正六边形A4B4C4D4E4F4的面积是.
21. 如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2 , 如此继续下去,则正六边形A4B4C4D4E4F4的面积是.
三、综合题
-
22. 问题的提出:n个平面最多可以把空间分割成多少个部分?
问题的转化:由n上面问题比较复杂,所以我们先来研究跟它类似的一个较简单的问题:
n条直线最多可以把平面分割成多少个部分?
如图1,很明显,平面中画出1条直线时,会得到1+1=2个部分;所以,1条直线最多可以把平面分割成2个部分;
如图2,平面中画出第2条直线时,新增的一条直线与已知的1条直线最多有1个交点,这个交点会把新增的这条直线分成2部分,从而多出2个部分,即总共会得到1+1+2=4个部分,所以,2条直线最多可以把平面分割成4个部分;
如图3,平面中画出第3条直线时,新增的一条直线与已知的2条直线最多有2个交点,这2个交点会把新增的这条直线分成3部分,从而多出3个部分,即总共会得到1+1+2+3=7个部分,所以,3条直线最多可以把平面分割成7个部分;
平面中画出第4条直线时,新增的一条直线与已知的3条直线最多有3个交点,这3个交点会把新增的这条直线分成4部分,从而多出4个部分,即总共会得到1+1+2+3+4=11个部分,所以,4条直线最多可以把平面分割成11个部分;…
 (1)、请你仿照前面的推导过程,写出“5条直线最多可以把平面分割成多少个部分”的推导过程(只写推导过程,不画图);
(1)、请你仿照前面的推导过程,写出“5条直线最多可以把平面分割成多少个部分”的推导过程(只写推导过程,不画图);
(2)、根据递推规律用n的代数式填空:n条直线最多可以把平面分割成个部分.问题的解决:借助前面的研究,我们继续开头的问题;n个平面最多可以把空间分割成多少个部分?
首先,很明显,空间中画出1个平面时,会得到1+1=2个部分;所以,1个平面最多可以把空间分割成2个部分;
空间中有2个平面时,新增的一个平面与已知的1个平面最多有1条交线,这1条交线会把新增的这个平面最多分成2部分,从而多出2个部分,即总共会得到1+1+2=4个部分,所以,2个平面最多可以把空间分割成4个部分;
空间中有3个平面时,新增的一个平面与已知的2个平面最多有2条交线,这2条交线会把新增的这个平面最多分成4部分,从而多出4个部分,即总共会得到1+1+2+4=8个部分,所以,3个平面最多可以把空间分割成8个部分;
空间中有4个平面时,新增的一个平面与已知的3个平面最多有3条交线,这3条交线会把新增的这个平面最多分成7部分,从而多出7个部分,即总共会得到1+1+2+4+7=15个部分,所以,4个平面最多可以把空间分割成15个部分;
空间中有5个平面时,新增的一个平面与已知的4个平面最多有4条交线,这4条交线会把新增的这个平面最多分成11部分,而从多出11个部分,即总共会得到1+1+2+4+7+11=26个部分,所以,5个平面最多可以把空间分割成26个部分;…
(3)、请你仿照前面的推导过程,写出“6个平面最多可以把空间分割成多少个部分?”的推导过程(只写推导过程,不画图);(4)、根据递推规律填写结果:10个平面最多可以把空间分割成个部分;(5)、设n个平面最多可以把空间分割成Sn个部分,设n﹣1个平面最多可以把空间分割成Sn﹣1个部分,前面的递推规律可以用Sn﹣1和n的代数式表示Sn;这个等式是Sn= .23. 观察下列等式:第一个等式:
第二个等式:
第三个等式:
第四个等式:
按上述规律,回答下列问题:
(1)、请写出第六个等式:a6==;(2)、用含n的代数式表示第n个等式:an==;(3)、a1+a2+a3+a4+a5+a6=(得出最简结果);(4)、计算:a1+a2+…+an .24. 观察下列各个等式的规律:第一个等式: =1,第二个等式: =2,第三个等式: =3…
请用上述等式反映出的规律解决下列问题:
(1)、直接写出第四个等式;(2)、猜想第n个等式(用n的代数式表示),并证明你猜想的等式是正确的.25.问题提出:用水平线和竖直线将平面分成若干个面积为1的小长方形格子,小长方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x,多边形内部的格点数为n,S与x,n之间是否存在一定的数量关系呢?
 (1)、问题探究:
(1)、问题探究:如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S= .
多边形的序号
①
②
③
④
…
多边形的面积S
2
2.5
3
4
…
各边上格点的个数和x
4
…
(2)、在图2中所示的格点多边形,这些多边形内部都有且只有2个格点.探究此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S= .(3)、请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=(用含有字母x,n的代数式表示)(4)、问题拓展:请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:
格点多边形各边上的格点的个数
格点多边形内部的格点个数
格点多边形的面积
多边形1(图3)
8
1
8
多边形2(图4)
7
3
11
…
…
…
…
…
…
…
…
…
…
…
…
一般格点多边形
a
b
S
则S与a,b之间的关系为S=(用含a,b的代数式表示).