江苏省扬州市江都区邵樊片2016-2017学年八年级下学期数学期中考试试卷

试卷更新日期：2018-04-13 类型：期中考试

进入出卷网下载

一、单选题

1. 完成下列任务，宜用抽样调查的是（）

A、调查你班同学的年龄情况 B、了解你所在学校男、女生人数 C、考察一批炮弹的杀伤半径 D、奥运会上对参赛运动员进行的尿样检查

查看试题解析
2. 若分式 $\frac{2}{x - 1}$ 有意义，则x的取值范围是（）

A、x≠1 B、x＞1 C、x=1 D、x＜1

查看试题解析
3. 下列图案中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 为了了解某县八年级学生的体重情况，从中抽取了200名学生进行体重测试.在这个问题中，下列说法错误的是（）

A、200名学生的体重是总体 B、200名学生的体重是一个样本 C、每个学生的体重是一个个体 D、全县八年级学生的体重是总体。

查看试题解析
5. 如果把分式 $\frac{2 x y}{x + y}$ 中的x和y都扩大3倍，那么分式的值（）

A、不变 B、缩小3倍 C、扩大6倍 D、扩大3倍

查看试题解析
6. 菱形具有而矩形不一定具有的性质是（　　）

A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补

查看试题解析
7. 如图，一个四边形花坛ABCD，被两条线段MN，EF分成四个部分，分别种上红、黄、紫、白四种花卉，种植面积依次是S₁ ， S₂ ， S₃ ， S₄ ，若MN∥AB∥CD，EF∥DA∥CB，则有（）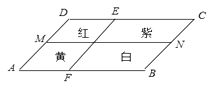

A、S₁=S₄ B、S₁+S₄=S₂+S₃ C、S₁S₄=S₂S₃ D、都不对

查看试题解析
8. 已知关于x的分式方程 $\frac{5}{x} = \frac{a}{x - 2}$ 有解，则字母a的取值范围是（）

A、a＝5或a＝0 B、a≠0 C、a≠5 D、a≠5且a≠0

查看试题解析

二、填空题

9. 某中学数学教研组有25名教师，将他们按年龄分组，在38~45岁组内的教师有8名教师，那么这个小组的频率是。

查看试题解析
10. 当x＝时，分式 $\frac{x^{2} - 16}{x + 4}$ 的值为零。

查看试题解析
11. 小芳掷一枚硬币 $10$ 次，有 $7$ 次正面向上，当她掷第 $11$ 次时，正面向上的概率为.

查看试题解析
12. 如图，在四边形ABCD中，AB∥CD，要使得四边形ABCD是平行四边形，应添加的条件是．（只填写一个条件，不另外添加字母和线段）

查看试题解析
13. △ABC三边的中点分别为D、E、F，如果AB=6cm，AC=8cm，BC=10cm，那么△DEF的面积是cm。

查看试题解析
14. 关于x的分式方程 $\frac{m}{x + 1}$ ＝－1的解是负数，则m的取值范围是。

查看试题解析
15. 已知ab=1，M= $\frac{1}{1 + a} + \frac{1}{1 + b}$ ，N= $\frac{a}{1 + a} + \frac{b}{1 + b}$ ，则MN。（填“＜”、“＞”或“＝”）.

查看试题解析
16. 若关于x的分式方程 $\frac{2 m + x}{x - 3} - 1 = \frac{2}{x}$ 有增根，则该方程的增根为。

查看试题解析
17. 甲、乙、丙三人进行乒乓球比赛，规则是：两人比赛，另一人当裁判，输者将在下一局中担任裁判，每一局比赛没有平局．已知甲、乙各比赛了4局，丙当了3次裁判．则第二局的输者是。

查看试题解析
18. 如图，Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC= $\frac{5}{6}$ ，OC= $\sqrt{2}$ ，则另一直角边BC的长为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\frac{x}{x + 1} + \frac{x + 2}{x + 1}$ ；

(2)、 $\frac{2 x}{x + 1} - \frac{2 x + 6}{x^{2} - 1} \div \frac{x + 3}{x^{2} - 2 x + 1}$ .

查看试题解析
20. 解方程：

(1)、 $1 + \frac{3 x}{x - 2} = \frac{6}{x - 2}$ ；

(2)、 $\frac{1}{2 x - 1} = \frac{1}{2} - \frac{3}{4 x - 2}$ ；

查看试题解析
21. 如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：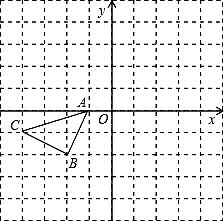

(1)、①以A点为旋转中心，将△ABC绕点A顺时针旋转90°得△AB₁C₁ ，画出△AB₁C₁ ．
②作出△ABC关于坐标原点O成中心对称的△A₂B₂C₂ ．

(2)、作出点C关于x轴的对称点P．若点P向右平移x（x取整数）个单位长度后落在△A₂B₂C₂的内部，请直接写出x的值．

查看试题解析
22. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
摸球的次数 $n$
100
200
300
500
800
1000
3000
摸到白球的次数 $m$
65
124
178
302
481
599
1803
摸到白球的频率 $\frac{m}{n}$
0.65
0.62
0.593
0.604
0.601
0.599
0.601

(1)、请估计：当 $n$ 很大时，摸到白球的频率将会接近．（精确到0.1）

(2)、假如你摸一次，你摸到白球的概率P_（白球）= ．

(3)、试估算盒子里黑、白两种颜色的球各有多少只？

查看试题解析
23. 如图， $E、F$ 是平行四边形ABCD的对角线 AC上的点，CE=AF ，请你猜想：线段 BE 与线段 $DF$ 有怎样的关系？并对你的猜想加以证明。

查看试题解析
24. 某校为了了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：kg）分成五组（A：39.5～46.5；B：46.5～53.5；C：53.5～60.5；D：60.5～67.5；E：67.5～74.5），并依据统计数据绘制了如下两幅尚不完整的统计图．
解答下列问题：

(1)、这次抽样调查的样本容量是，并补全频数分布直方图；

(2)、C组学生的频率为，在扇形统计图中D组的圆心角是度；

(3)、请你估计该校初三年级体重超过60kg的学生大约有多少名？

查看试题解析
25. 某部队将在指定山区进行军事演习，为了使道路便于部队重型车辆通过，部队工兵连接到抢修一段长3600米道路的任务，按原计划完成总任务的 $\frac{1}{3}$ 后，为了让道路尽快投入使用，工兵连将工作效率提高了50%，一共用了10小时完成任务．

(1)、按原计划完成总任务的 $\frac{1}{3}$ 时，已抢修道路米；

(2)、求原计划每小时抢修道路多少米？

查看试题解析
26. 如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．

(1)、判断OE与OF的大小关系？并说明理由；

(2)、当点O运动到何处时，四边形AECF是矩形？并说出你的理由；

(3)、在（2）的条件下，当△ABC满足什么条件时，四边形AECF是正方形．直接写出答案，不需说明理由。

查看试题解析
27. 在边长为1的菱形ABCD中，动点M从点A出发，沿A→B→C向终点C运动，连接DM交AC于点N.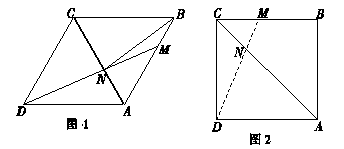

(1)、如图1，当点M在AB边上时，连接BN.求证：△ABN≌△ADN；

(2)、如图2，若∠ABC=90°，记点M运动所经过的路程为x（1≤x≤2）试问：x为何值时，△ADN为等腰三角形．

查看试题解析
28. 我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．

(1)、写出你所学过的特殊四边形中是勾股四边形的两种图形的名称，；

(2)、如图1，已知格点（小正方形的顶点）O（0，0），A（3，0），B（0，4），请你直接写出所有以格点为顶点，OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标．

(3)、如图2，将△ABC绕顶点B按顺时针方向旋转60°，得到△DBE，连接AD、DC，∠DCB=30°．求证：DC²+BC²=AC² ，即四边形ABCD是勾股四边形．

(4)、若将图2中△ABC绕顶点B按顺时针方向旋转a度（0°＜a＜90°），得到△DBE，连接AD、DC，则∠DCB=°，四边形ABCD是勾股四边形．

查看试题解析

摸球的次数 $n$	100	200	300	500	800	1000	3000
摸到白球的次数 $m$	65	124	178	302	481	599	1803
摸到白球的频率 $\frac{m}{n}$	0.65	0.62	0.593	0.604	0.601	0.599	0.601