备考2018年中考数学一轮基础复习：专题二十四 收据的收集与整理
试卷更新日期：2018-04-12 类型：一轮复习
一、单选题
-
1. 下列说法正确的是（ ）A、要了解某公司生产的100万只灯泡的使用寿命，可以采用抽样调查的方法 B、4位同学的数学期末成绩分别为100、95、105、110，则这四位同学数学期末成绩的中位数为100 C、甲乙两人各自跳远10次，若他们跳远成绩的平均数相同，甲乙跳远成绩的方差分别为0.51和0.62 D、某次抽奖活动中，中奖的概率为 表示每抽奖50次就有一次中奖2. 下列说法正确的是（ ）A、打开电视，它正在播广告是必然事件 B、要考察一个班级中的学生对建立生物角的看法适合用抽样调查 C、在抽样调查过程中，样本容量越大，对总体的估计就越准确 D、甲、乙两人射中环数的方差分别为S甲2=2，S乙2=4，说明乙的射击成绩比甲稳定3. 下列说法正确的是（ ）A、“打开电视机，正在播放体育节目”是必然事件 B、了解夏季冷饮市场上冰淇淋的质量情况适合用普查 C、抛掷一枚普通硬币，“这枚硬币正面朝上”，这一事件发生的概率为 D、甲、乙两人在相同条件下各射击10次，他们的成绩的平均数相同，方差分别是S甲2=0.3，S乙2=0.5，则乙的射击成绩较稳定4. 下列调查中，适宜采用全面调查（普查）方式的是（ ）A、了解我国民众对乐天集团“萨德事件”的看法 B、了解湖南卫视《人们的名义》反腐剧的收视率 C、调查我校某班学生喜欢上数学课的情况 D、调查某类烟花爆竹燃放的安全情况5. 空气是混合物，为直观介绍空气各成分的百分比，最适合用的统计图是（ ）A、折线图 B、条形图 C、直方图 D、扇形图6. 某班学生积极参加献爱心活动，该班50名学生的捐款统计情况如下表：
金额/元
5
10
20
50
100
人数
4
16
15
9
6
则他们捐款金额的中位数和平均数分别是（ ）
A、10，20.6 B、20，20.6 C、10，30.6 D、20，30.67.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图．那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是（ ）
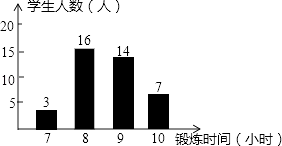A、16，10.5 B、8，9 C、16，8.5 D、8，8.58. 甲、乙、丙、丁四名射击运动员在选选拔赛中，每人射击了10次，甲、乙两人的成绩如表所示．丙、丁两人的成绩如图所示．欲选一名运动员参赛，从平均数与方差两个因素分析，应选（ ）甲
乙
平均数
9
8
方差
1
1
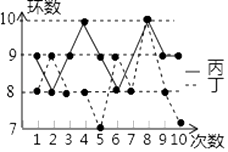A、甲 B、乙 C、丙 D、丁9. 下列说法正确的是（ ）A、检测某批次灯泡的使用寿命，适宜用全面调查 B、可能性是1%的事件在一次试验中一定不会发生 C、数据3，5，4，1，﹣2的中位数是4 D、“367中有2人同月同日初生”为必然事件10. 如图，是根据某市2010年至2014年工业生产总值绘制的折线统计图，观察统计图获得以下信息，其中信息判断错误的是（ ）
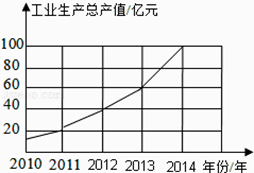A、2010年至2014年间工业生产总值逐年增加 B、2014年的工业生产总值比前一年增加了40亿元 C、2012年与2013年每一年与前一年比，其增长额相同 D、从2011年至2014年，每一年与前一年比，2014年的增长率最大11. 为估计鱼塘中的鱼的数量，可以先从鱼塘中随机打捞50条鱼，在每条鱼身上做上记号后，把这些鱼放归鱼塘，经过一段时间，等这些鱼完全混合于鱼群后，再从鱼塘中随机打捞50条鱼，发现只有2条鱼是前面做好记号的，那么可以估计这个鱼塘鱼的数量约为（ ）A、1250条 B、1750条 C、2500条 D、5000条12. 下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况．2011﹣2016年我国与东南亚地区和东欧地区的贸易额统计图
（以上数据摘自《“一带一路”贸易合作大数据报告（2017）》）
根据统计图提供的信息，下列推理不合理的是（ ）
A、与2015年相比，2016年我国与东欧地区的贸易额有所增长 B、2011﹣2016年，我国与东南亚地区的贸易额逐年增长 C、2011﹣2016年，我国与东南亚地区的贸易额的平均值超过4200亿美元 D、2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多13. 为了解中考体育科目训练情况，某校从九年级学生中随机抽取部分学生进行了一次中考体育科目测试（把测试结果分为A，B，C，D四个等级），并将测试结果绘制成了如图所示的两幅不完整统计图，根据统计图中提供的信息，结论错误的是（ ）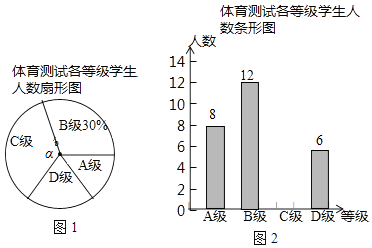
A、本次抽样测试的学生人数是40 B、在图1中，∠α的度数是126° C、该校九年级有学生500名，估计D级的人数为80 D、从被测学生中随机抽取一位，则这位学生的成绩是A级的概率为0.214. 为了鼓励学生课外阅读，学校公布了“阅读奖励”方案，并设置了“赞成、反对、无所谓”三种意见．现从学校所有 名学生中随机征求了 名学生的意见，其中持“反对”和“无所谓”意见的共有 名学生，估计全校持“赞成”意见的学生人数约为（ ）
A、 B、 C、 D、15. 根据下表中的信息解决问题：数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（ ）
A、3个 B、4个 C、5个 D、6个二、填空题
-
16. 为了调查某市中小学生对“营养午餐”的满意程度，适合采用的调查方式是 ． （填“全面调查”或“抽样调查”）
17. 如图是小强根据全班同学喜爱四类电视节目的人数而绘制的两幅不完整的统计图，则喜爱“体育”节目的人数是人．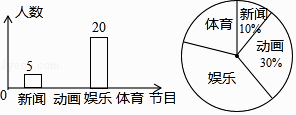
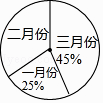
18.某企业今年第一季度各月份产值占这个季度总产值的百分比如图所示，又知二月份产值是72万元，那么该企业第一季度月产值的平均数是万元．
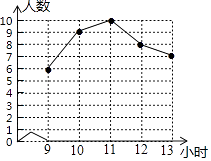
19. 红树林中学共有学生1600人，为了解学生最喜欢的课外体育运动项目的情况，学校随机抽查了200名学生，其中有85名学生表示最喜欢的项目是跳绳，则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有人．20.某班体育委员对本班学生一周锻炼时间（单位：小时）进行了统计，绘制了如图所示的折线统计图，则该班这些学生一周锻炼时间的中位数是小时．
21. 学习委员调查本班学生课外阅读情况，对学生喜爱的书籍进行分类统计，其中“古诗词类”的频数为12人，频率为0.25，那么被调查的学生人数为 ．三、综合题
-
22. 某初级中学正在展开“文明城市创建人人参与，志愿服务我当先行”的“创文活动”为了了解该校志愿者参与服务情况，现对该校全体志愿者进行随机抽样调查．根据调查数据绘制了如下所示不完整统计图．条形统计图中七年级、八年级、九年级、教师分别指七年级、八年级、九年级、教师志愿者中被抽到的志愿者，扇形统计图中的百分数指的是该年级被抽到的志愿者数与样本容量的比．
(1)、请补全条形统计图；(2)、若该校共有志愿者600人，则该校九年级大约有多少志愿者？23.某校举办了一次成语知识竞赛，满分10分，学生得分均为整数，成绩达到6分及6分以上为合格，达到9分或10分为优秀，这次竞赛中，甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示．
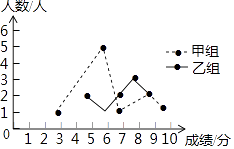(1)、求出下列成绩统计分析表中a，b的值：组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(2)、小英同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察上面表格判断，小英是甲、乙哪个组的学生；(3)、甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你写出两条支持乙组同学观点的理由．24. 某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整．收集数据
从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下：
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据：
成绩x
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
（说明：成绩80分及以上为生产技能优秀，70﹣﹣79分为生产技能良好，60﹣﹣69分为生产技能合格，60分以下为生产技能不合格）
分析数据
两组样本数据的平均数、中位数、众数如下表所示：
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
得出结论：a．估计乙部门生产技能优秀的员工人数为；b．可以推断出部门员工的生产技能水平较高，理由为 ． （至少从两个不同的角度说明推断的合理性）
25.在全体丽水人民的努力下，我市剿灭劣V类水“河道清淤”工程取得了阶段性成果，下面的右表是全市十个县（市、区）指标任务数的统计表；左图是截止2017年3月31日和截止5月4日，全市十个县（市、区）指标任务累计完成数的统计图.
(1)、截止3月31日，完成进度（完成进度=累计完成数÷任务数×100%）最快、电慢的县（市、区）分别是哪一个？(2)、求截止5月4日全市的完成进度；(3)、请结合图形信息和数据分析，对I且完成指标任务的行动过程和成果进行评价.