2015-2016学年山东省济宁市微山县七年级下学期期中数学试卷
试卷更新日期：2016-12-01 类型：期中考试
一、选择题
-
1. 4的算术平方根是（ ）A、2 B、﹣2 C、±2 D、2. 如图，三条直线l1 ， l2 ， l3相交于点E，则∠1+∠2+∠3=（ ）
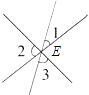A、90° B、120° C、180° D、360°3. 在实数0、n、 、 、﹣ 中，无理数的个数有（ ）A、1个 B、2个 C、3个 D、4个4.如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（ ）
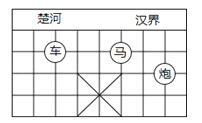A、（3，2） B、（﹣3，2） C、（3，﹣2） D、（﹣3，﹣2）5.如图，点E在BC的延长线上，下列条件中不能判定AB∥CD的是（ ）
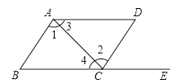A、∠3=∠4 B、∠1=∠2 C、∠B=∠DCE D、∠D+∠DAB=180°6. 有下列三个命题：（1）两点之间线段最短
（2）平面内，过一点能且只能作一条直线与已知直线垂直
（3）过直线外一点有且只有一条直线与这条直线平行
其中真命题的个数是（ ）
A、0个 B、1个 C、2个 D、3个7. 若点A（2，﹣2），B（﹣1，﹣2），则直线AB与x轴和y轴的位置关系分别是（ ）A、相交，相交 B、平行，平行 C、平行，垂直相交 D、垂直相交，平行8. 已知点A（1，0），B（0，2），点P在x轴上，且△PAB的面积为5，则点P的坐标为（ ）A、（﹣4，0） B、（6，0） C、（﹣4，0）或（6，0） D、无法确定9. 同一平面内，三条不同直线的交点个数可能是（ ）个．A、1或3 B、0、1或3 C、0、1或2 D、0、1、2或310. 如图，直径为1个单位长度的圆从A点沿数轴向右滚动（无滑动）两周到达点B，则点B表示的数是（ ）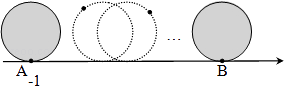
A、π B、2π C、2π﹣1 D、2π+1．二、填空
-
11. ﹣1的相反数是 ．12. 直线m外有一定点A，A到直线m的距离是7cm，B是直线m上的任意一点，则线段AB的长度：AB7cm．（填＞或者＜或者=或者≤或者≥）．13. 若一个正数的平方根是2a﹣1和﹣a+2，则这个正数是 ．14. 线段AB两端点的坐标分别为A（2，4），B（5，2），若将线段AB平移，使得点B的对应点为点C（3，﹣1）．则平移后点A的对应点的坐标为15. 点P到x轴的距离是2，到y轴的距离是3，且点P在y轴的右侧，则P点的坐标是 ．
三、解答
-
16. 计算：(1)、﹣ ﹣4
(2)、已知：x，y为实数，且满足|x+3|+ =0，求：代数式| +x|+ 的值．17. 如图，已知∠1=∠2，∠B=∠C，试证明AB∥CD．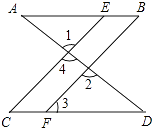
18. 如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2），
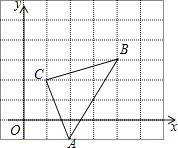(1)、写出点A，B的坐标：A（ ， ）、B（ ， ）(2)、将△ABC先向左平移1个单位长度，再向上平移2个单位长度，得到△A′B′C′，画出△A′B′C′(3)、写出三个顶点坐标A′（、）、B′（、）、C′、）(4)、求△ABC的面积．19. 如图，在A，B两处之间要修一条笔直的公路，从A地测得公路走向是北偏东46°，A，B两地同时开工，若干天后公路准确接通．
(1)、B地修公路的走向是南偏西多少度？(2)、若公路AB长12千米，另一条公路BC长6千米，且BC的走向是北偏西44°，试求A到公路BC的距离？20. 在平面直角坐标系中，点A的坐标是（3a﹣5，a+1）(1)、若点A在y轴上，求a的值及点A的坐标．(2)、若点A到x轴的距离与到y轴的距离相等；求a的值及点A的坐标．21. 阅读理解∵ ＜ ＜ ，即2＜ ＜3．
∴ 的整数部分为2，小数部分为 ﹣2
∴1＜ ﹣1＜2
∴ ﹣1的整数部分为1．
∴ ﹣1的小数部分为 ﹣2
解决问题：已知：a是 ﹣3的整数部分，b是 ﹣3的小数部分，求：
(1)、a，b的值；(2)、（﹣a）3+（b+4）2的平方根．22. 如图（1），AB∥CD，猜想∠BPD与∠B，∠D的关系，说出理由．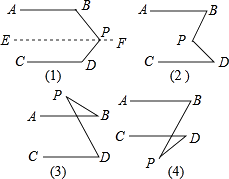
解：猜想∠BPD+∠B+∠D=360°
理由：过点P作EF∥AB，
∴∠B+∠BPE=180°（两直线平行，同旁内角互补）
∵AB∥CD，EF∥AB，
∴EF∥CD，（如果两条直线都和第三条直线平行，那么这两条直线也互相平行．）
∴∠EPD+∠D=180°（两直线平行，同旁内角互补）
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)、依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B，∠D的关系，并说明理由．(2)、观察图（3）和（4），已知AB∥CD，猜想图中的∠BPD与∠B，∠D的关系，不需要说明理由．