四川省简阳市2017届九年级下学期数学期中考试试卷

试卷更新日期：2018-04-10 类型：期中考试

进入出卷网下载

一、单选题

1. －5的相反数是（）

A、－5 B、5 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 下列运算正确的是（）

A、（ab）⁵=ab⁵ B、a⁸÷a²=a⁶ C、（a²）³=a⁵ D、（a﹣b）²=a²﹣b²

查看试题解析
3. 将一张正方形纸片如图所示折叠两次，并在上面剪下一个菱形小洞，纸片展开后是（）（填序号）．

A、① B、② C、③ D、④

查看试题解析
4. 资阳市2012年财政收入取得重大突破，地方公共财政收入用四舍五入取近似值后为27.39亿元，那么这个数值（）

A、精确到亿位 B、精确到百分位 C、精确到千万位 D、精确到百万位

查看试题解析
5. 如图，已知数轴上的点A，B，C，D分别表示数﹣2、1、2、3，则表示数3﹣ $\sqrt{5}$ 的点P应落在（）

A、线段AO上 B、线段OB上 C、线段BC上 D、线段CD上

查看试题解析
6. 甲、乙两名同学进行了6轮投篮比赛，两人的得分情况统计如下：
下列说法不正确的是（）

A、甲得分的极差小于乙得分的极差 B、甲得分的中位数大于乙得分的中位数 C、甲得分的平均数大于乙得分的平均数 D、乙的成绩比甲的成绩稳定

查看试题解析
7. 在某校校园文化建设活动中，小彬同学为班级设计了一个班徽，这个班徽图案由一对大小相同的较大半圆挖去一对大小相同的较小半圆而得．如图，若它们的直径在同一直线上，较大半圆O₁的弦AB∥O₁O₂ ，且与较小半圆O₂相切， AB=4，则班徽图案的面积为（）

A、 $25 π$ B、 $16 π$ C、 $8 π$ D、 $4 π$

查看试题解析
8. 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（）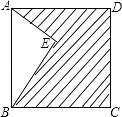

A、48 B、60 C、76 D、80

查看试题解析
9. 如图，矩形ABCD的对角线AC，BD相交于点O，过点O作OE⊥AC交AB于E，若BC=4，△AOE的面积为5，则sin∠BOE的值为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac-b²＜0；②4a+c＜2b；③3b+2c＜0；④m（am+b）+b＜a（m≠﹣1），其中正确结论的个数是（）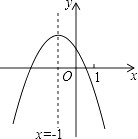

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

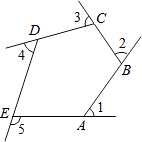
11. 已知α、β均为锐角，且满足|sinα﹣ $\frac{1}{2}$ |+ $\sqrt{{(tan β - 1)}^{2}}$ =0，则α+β= ．

查看试题解析
12. 如图是由射线AB，BC，CD，DE，EA组成的平面图形，则∠1+∠2+∠3+∠4+∠5= ．

查看试题解析
13. 如图是一次函数的 $y = k x + b$ 图象，则关于x的不等式 $k x + b > 0$ 的解集为．

查看试题解析
14. 商店某天销售了ll件衬衫，其领口尺寸统计如下表：
领口尺寸（单位：cm）
38
39
40
41
42
件数
1
4
3
1
2
则这ll件衬衫领口尺寸的众数是 cm，中位数是 cm．

查看试题解析
15. 已知 $a_{n} = \frac{1}{{(n + 1)}^{2}} (n = 1 ， 2 ， 3 ， ...)$ ，记 $b_{1} = 2 (1 - a_{1})$ ， $b_{2} = 2 (1 - a_{1}) (1 - a_{2})$ ，…， $b_{n} = 2 (1 - a_{1}) (1 - a_{2}) ... (1 - a_{n})$ ，则通过计算推测出 $b_{n}$ 的表达式 $b_{n}$ ＝． (用含n的代数式表示)

查看试题解析
16. 如图，Rt△ABC中，AC⊥BC，AD平分∠BAC交BC于点D，DE⊥AD交AB于点E，M为AE的中点，BF⊥BC交CM的延长线于点F，BD=4，CD=3．下列结论：①∠AED=∠ADC；② $\frac{D E}{D A}$ = $\frac{3}{4}$ ；③AC•BE=12；④3BF=4AC，其中结论正确的是（填序号）

查看试题解析

三、解答题

17. 化简求值： $(\frac{3}{x - 1} - x - 1) \div \frac{x - 2}{x^{2} - 2 x + 1}$ ，其中 $x = - \sqrt{2}$ ．

查看试题解析
18. 第十五届中国“西博会”将于2014年10月底在成都召开，现有20名志愿者准备参加某分会场的工作，其中男生8人，女生12人.

(1)、若从这20人中随机选取一人作为联络员，求选到女生的概率；

(2)、若该分会场的某项工作只在甲、乙两人中选一人，他们准备以游戏的方式决定由谁参加，游戏规则如下：将四张牌面数字分别为2、3、4、5的扑克牌洗匀后，数字朝下放于桌面，从中任取2张，若牌面数字之和为偶数，则甲参加，否则乙参加.试问这个游戏公平吗？请用树状图或列表法说明理由.

查看试题解析
19. 现有A，B两种商品，买2件A商品和1件B商品用了90元，买3件A商品和2件B商品共用了160元.

(1)、求A，B两种商品每件多少元？

(2)、如果小亮准备购买A，B两种商品共10件，总费用不超过350元，且不低于300元，问有几种购买方案，哪种方案费用最低？

查看试题解析
20. 如图，在Rt△ABC中，∠ABC＝90°，以CB为半径作⊙C，交AC于点D，交AC的延长线于点E，连接ED，BE．

(1)、求证：△ABD∽△AEB；

(2)、当 $\frac{A B}{B C} = \frac{4}{3}$ 时，求tanE；

查看试题解析
21. 如图，一次函数y=kx+b的图象与反比例函数 $y = \frac{m}{x}$ （x＞0）的图象交于A（2，﹣1），B（ $\frac{1}{2}$ ，n）两点，直线y=2与y轴交于点C．

(1)、求一次函数与反比例函数的解析式；

(2)、求△ABC的面积．

查看试题解析
22. 每年的农历三月初一为通州风筝节．这天，小刘同学正在江海明珠广场上放风筝，如图风筝从A处起飞，几分钟后便飞达C处，此时，在AQ延长线上B处的小宋同学，发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.

(1)、已知旗杆高为10米，若在B处测得旗杆顶点P的仰角为30°，A处测得点P的仰角为45°，试求A、B之间的距离；

(2)、此时，在A处背向旗杆又测得风筝的仰角为75°，若绳子在空中视为一条线段，求绳子AC为多少米？（结果可保留根号）

查看试题解析
23. 如图①，△ABC中，∠ABC＝45°，AH⊥BC于点H，点D在AH上，且DH＝CH，连接BD.

(1)、求证：BD=AC；

(2)、将△BHD绕点H旋转，得到△EHF（点B，D分别与点E，F对应），连接AE.
ⅰ）如图②，当点F落在AC上时（F不与C重合），若BC＝4，tanC=3，求AE的长；
ⅱ）如图③，当△EHF是由△BHD绕点H逆时针旋转30°得到时，设射线CF与AE相交于点G，连接GH，试探究线段GH与EF之间满足的等量关系，并说明理由。

查看试题解析
24. 如图，已知抛物线y=ax²+bx+c经过A（﹣3，0），B（1，0），C（0，3）三点，其顶点为D，对称轴是直线l，l与x轴交于点H．

(1)、求该抛物线的解析式；

(2)、若点P是该抛物线对称轴l上的一个动点，求△PBC周长的最小值；

(3)、如图（2），若E是线段AD上的一个动点（ E与A、D不重合），过E点作平行于y轴的直线交抛物线于点F，交x轴于点G，设点E的横坐标为m，△ADF的面积为S．
①求S与m的函数关系式；
②S是否存在最大值？若存在，求出最大值及此时点E的坐标；若不存在，请说明理由．

查看试题解析

领口尺寸（单位：cm）	38	39	40	41	42
件数	1	4	3	1	2