四川省仁寿县龙正学区2016-2017学年八年级下学期数学期中考试试卷

试卷更新日期：2018-04-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，不是分式是（）

A、 $- \frac{3 a}{b}$ B、 $\frac{x}{π + 1}$ C、 $\frac{1}{2 x + y}$ D、 $\frac{x y}{x + y}$

查看试题解析
2. 实验表明，人体内某种细胞的形状科近似地看做球，它的直径约为0.00000156m，则这个数用科学记数法表示是（）

A、0.156 $\times$ 10^-5 B、0.156 $\times$ 10⁵ C、1.56 $\times$ 10^-6 D、1.56 $\times$ 10⁶

查看试题解析
3. 若分式 $\frac{2 - | x |}{x + 2}$ 的值为0，则x的值为（ )

A、0 B、2 C、-2 D、2或-2

查看试题解析
4. 已知一次函数 $y = \frac{3}{2} x + m$ 和 $y = - \frac{3}{2} x + n$ 的图像都经过点A（-2，0）且与y轴分别交于B、C两点，那么△ABC的面积为（）

A、2 B、3 C、4 D、6

查看试题解析
5. 函数 $y = \frac{\sqrt{x + 2}}{x - 1}$ 中自变量 $x$ 的取值范围是（）

A、 $x$ ≥-2 B、 $x$ ≥-2且 $x$ ≠1 C、 $x$ ≠1 D、 $x$ ≥-2或 $x$ ≠1

查看试题解析
6. 函数 $y = \frac{m}{x}$ 与y＝mx－m（m≠0）在同一平面直角坐标系中的大致图象是（）

A、 B、 C、 D、

查看试题解析
7. 张老师和李老师同时从学校出发，步行15千米去县城购买书籍，张老师比李老师每小时多走1千米，结果比李老师早到半小时，两位老师每小时各走多少千米？设李老师每小时走x千米，依题意，得到的方程是（）

A、 $\frac{15}{x + 1} - \frac{15}{x} = \frac{1}{2}$ B、 $\frac{15}{x} - \frac{15}{x + 1} = \frac{1}{2}$ C、 $\frac{15}{x - 1} - \frac{15}{x} = \frac{1}{2}$ D、 $\frac{15}{x} - \frac{15}{x - 1} = \frac{1}{2}$

查看试题解析
8. 在平面直角坐标系中， ▱ABCD的顶点A（0，0），B（5，0），D（2，3），则顶点C的坐标是（）

A、（3，7） B、（5，3） C、（7，3） D、（8，2）

查看试题解析
9. 如图，点P为▱ABCD的边CD上一点，若△PAB，△PCD，△PBC的面积分别为S₁、S₂和S₃ ，则它们之间的大小关系是（）

A、S₃＝S₁＋S₂ B、2S₃＝S₁＋S₂ C、S₃＞S₁＋S₂ D、S₃＜S₁＋S₂

查看试题解析
10. 如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x＝9时，点R应运动到（）

A、N处 B、P处 C、Q处 D、M处

查看试题解析
11. 若点（x₁ ， y₁）、（x₂ ， y₂）和（x₃ ， y₃）分别在反比例函数 $y = - \frac{2}{x}$ 的图象上， $x_{1} < x_{2} < 0 < x_{3}$ ，则下列判断中正确的是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
12. 如图，A，B 两点在反比例函数 $y = \frac{k_{1}}{x}$ 的图像上，C、D 两点在反比例函数 $y = \frac{k_{2}}{x}$ 的图像上，AC 交 x 轴于点 E，BD 交 x 轴于点 F， AC=2 ，BD=3 ，EF= $\frac{10}{3}$ 则k₂-k₁=（）

A、4 B、 $\frac{14}{3}$ C、 $\frac{16}{3}$ D、6

查看试题解析

二、填空题

13. 若方程 $\frac{6}{(x + 1) (x - 1)} - \frac{m}{x - 1} = 1$ 有增根，则它的增根是， m=；

查看试题解析
14. ▱ABCD的周长为40㎝，对角线AC、BD相交于点O，△AOB的周长比△BOC的周长多4㎝，则AB＝㎝，BC＝㎝。

查看试题解析
15. 已知等腰三角形的周长为60cm，若底边长为 $y$ cm，一腰长为 $x$ cm.则 $y$ 与 $x$ 的函数关系式为自变量 $x$ 的取值范围是

查看试题解析
16. 已知关于x的方程 $\frac{2 x + m}{x + 2} = 3$ 的解是负数，则m的取值范围是．

查看试题解析
17. 如图，已知直线 $y = - 2 x + b$ 与直线 $y = a x - 1$ 相交于点（2，－2），由图象可得不等式 $- 2 x + b > a x - 1$ 的解集是。

查看试题解析
18. 正方形A₁B₁C₁O ， A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …按如图方式放置，点A₁、A₂、A₃…和点C₁、C₂、C₃…分别在直线 $y = k x + b (k > 0)$ 和x轴上。已知点B₁（1，1）、B₂（3，2），请写出点B₃的坐标是，点B_n的坐标是。

查看试题解析

三、解答题

19. 计算： ${(\frac{1}{2})}^{- 1} + | - 2 | - {(π - 1)}^{0}$

查看试题解析
20. 解方程： $\frac{2}{1 + x} - \frac{3}{1 - x} = \frac{6}{x^{2} - 1}$

查看试题解析
21. 阅读下面的对话。
小红：“售货员，我要买些梨。”
售货员说：“小红，你上次买的那种梨卖完了，我们还没来得及进货，我建议你这次买些新进的苹果，价格比梨贵一点，不过这批苹果的味道挺好哟！”
小红：“好，这次和上次一样，也花30元。”
对照前后两次的电脑小票，小红发现，每千克苹果的单价是梨的1.5倍，买的苹果的重量比梨轻2.5Kg。
试根据上面的对话和小红的发现，分别求出苹果和梨的单价。

查看试题解析
22. 已知：如图，在▱ABCD中，对角线AC ， BD交于点O ， AB⊥AC ， AB=1，BC= $\sqrt{5}$ ．

(1)、求平行四边形ABCD的面积S_▱ABCD；

(2)、求对角线BD的长．

查看试题解析
23. 已知，如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y= $\frac{n}{x}$ （n为常数且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂直为D，若OB=2OA=3OD=6．

(1)、求一次函数与反比例函数的解析式；

(2)、求两函数图象的另一个交点坐标；

(3)、直接写出不等式；kx+b≤ $\frac{n}{x}$ 的解集．

查看试题解析
24. 某水果积极计划装运甲、乙、丙三种水果到外地销售（每辆汽车规定满载，并且只装一种水果）．如表为装运甲、乙、丙三种水果的重量及利润．

甲
乙
丙
每辆汽车能装的数量（吨）
4
2
3
每吨水果可获利润（千元）
5
7
4

(1)、用8辆汽车装运乙、丙两种水果共22吨到A地销售，问装运乙、丙两种水果的汽车各多少辆？

(2)、水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售（每种水果不少于一车），假设装运甲水果的汽车为m辆，则装运乙、丙两种水果的汽车各多少辆？（结果用m表示）

(3)、在（2）问的基础上，如何安排装运可使水果基地获得最大利润？最大利润是多少？

查看试题解析
25. 如图，直线l₁的解析表达式为：y=-3x+3，且l₁与x轴交于点D，直线l₂经过点A，B，直线l₁ ， l₂交于点C．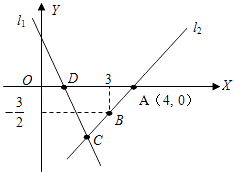

(1)、求点D的坐标；

(2)、求直线l₂的解析表达式；

(3)、求△ADC的面积；

(4)、在直线l₂上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．

查看试题解析
26. 甲、乙两车分别从相距480km的A、B两地相向而行，乙车比甲车先出发1小时，并以各自的速度匀速行驶，途径C地，甲车到达C地停留1小时，因有事按原路原速返回A地．乙车从B地直达A地，两车同时到达A地．甲、乙两车距各自出发地的路程y（千米）与甲车出发所用的时间x（小时）的关系如图，结合图象信息解答下列问题：

(1)、乙车的速度是千米/时，t＝小时；

(2)、求甲车距它出发地的路程y与它出发的时间x的函数关系式，并写出自变量的取值范围；

(3)、直接写出乙车出发多长时间两车相距120千米．

查看试题解析

	甲	乙	丙
每辆汽车能装的数量（吨）	4	2	3
每吨水果可获利润（千元）	5	7	4