福建省漳州市长泰县2016-2017学年八年级下学期数学期中考试试卷

试卷更新日期：2018-04-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式 $\frac{1}{x + 2 y}$ ， $\frac{5 a - b}{2 a - b}$ ， $\frac{3 a^{2} - b^{2}}{5}$ ， $\frac{3}{m}$ ， $\frac{3 x y}{7}$ 中，分式共有（）个．

A、2 B、3 C、4 D、5

查看试题解析
2. 若把分式 $\frac{x + y}{x y}$ 中的x和y都扩大3倍，那么分式的值（）

A、为原来的3倍 B、不变 C、为原来的 $\frac{1}{3}$ D、为原来的 $\frac{1}{6}$

查看试题解析
3. 在平面直角坐标系中，点（4，﹣3）关于y轴对称的点的坐标是（）

A、（﹣4，﹣3） B、（4，3） C、（﹣4，3） D、（4，﹣3）

查看试题解析
4. 花粉的质量很小，一粒某种植物花粉的质量约为0.000037毫克，那么0.000037毫克可用科学记数法表示为（）

A、3.7×10^﹣5毫克 B、3.7×10^﹣6毫克 C、37×10^﹣7毫克 D、3.7×10^﹣8毫克

查看试题解析
5. 某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时赶到了学校．如图描述了他上学的情景，下列说法中错误的是（）

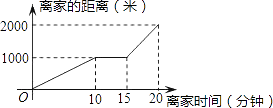A、修车时间为15分钟 B、学校离家的距离为2000米 C、到达学校时共用时间20分钟 D、自行车发生故障时离家距离为1000米

查看试题解析
6. 考察反比例函数y=﹣ $\frac{6}{x}$ ，下列结论中不正确的是（）

A、图象必经过（﹣3，2） B、当x＞0时，y随x的增大而增大 C、图象在第二、四象限内 D、图象与直线y=x有两个交点

查看试题解析
7. 一次函数y=kx+b，当k＞0，b＜0时，它的图象是（）

A、 B、 C、 D、

查看试题解析
8. 已知平行四边形ABCD中，∠B=5∠A，则∠C=（）

A、30° B、60° C、120° D、150°

查看试题解析
9. 如图，在平面直角坐标系中，▱AB的顶点A、B、D的坐标分别是(0，0)，(5，0)，(2，3)，则顶点C的坐标是（）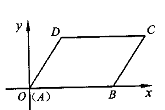

A、（3，7） B、（5，3） C、（7，3） D、（8，2）

查看试题解析
10. 若反比例函数y= $\frac{k}{x}$ （k＜0）的图象经过点（﹣2，y₁），（﹣1，y₂），（2，y₃），则y₁ ， y₂ ， y₃的大小关系为（）

A、y₁＞y₂＞y₃ B、y₁＞y₃＞y₂ C、y₂＞y₁＞y₃ D、y₃＞y₂＞y₁

查看试题解析
11. 如图，在平面直角坐标系中，直线l₁：y=x+3与直线l₂：y=mx+n交于点A（﹣1，b），则关于x、y的方程组 ${\begin{matrix} y = x + 3 \\ y = m x + n \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = - 1 \\ y = - 2 \end{matrix}$

查看试题解析
12. 如图，直线l⊥x轴于点P，且与反比例函数y₁= $\frac{k_{1}}{x}$ （x＞0）及y₂= $\frac{k_{2}}{x}$ （x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k₁﹣k₂的值为（）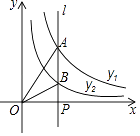

A、2 B、3 C、4 D、﹣4

查看试题解析

二、填空题

13. 在函数y= $\frac{x + 2}{x - 3}$ 中，自变量x的取值范围是．

查看试题解析
14. 当x=时，分式 $\frac{x^{2} - 4}{x + 2}$ 的值为零．

查看试题解析
15. 化简： $\frac{2 a}{a - b} + \frac{a + b}{b - a}$ = ．

查看试题解析
16. 计算：（﹣m³n^﹣2）^﹣2= ．（结果不含负整数指数幂）

查看试题解析
17. 一次函数y=kx+5的图象可由正比例函数y=2x的图象向上平移5个单位长度得到，则k= ．

查看试题解析
18. 一次函数y=（2m﹣6）x+4中，y随x的增大而减小，则m的取值范围是．

查看试题解析
19. 如图，在平行四边形ABCD中，BC=8cm，AB=6cm，BE平分∠ABC交AD边于点E，则线段DE的长度为．

查看试题解析
20. 如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD交BC于点E，若平行四边形ABCD的周长为20，则△CDE的周长为_ ．

查看试题解析

三、解答题

21. 计算：

(1)、（﹣ $\frac{1}{2}$ ）^﹣2+ $\sqrt[3]{27}$ ﹣（ $\sqrt{5}$ ﹣1）⁰；

(2)、（1+ $\frac{3}{x-1}$ ）÷ $\frac{x+2}{x^{2} - 1}$ ．

查看试题解析
22. 解方程： $\frac{2}{3 x-1} - 1 = \frac{3}{6 x-2}$

查看试题解析
23. 已知一次函数y=kx+b，当x=2时y的值是﹣1，当x=﹣1时y的值是5．

(1)、求此一次函数的解析式；

(2)、若点P（m，n）是此函数图象上的一点，﹣3≤m≤2，求n的最大值．

查看试题解析
24. 如图，▱ABCD中，对角线AC与BD相交于O，EF是过点O的任一直线交AD于点E，交BC于点F，猜想OE和OF的数量关系，并说明理由．

查看试题解析
25. 列方程或方程组解应用题
我区为缓解某景区的交通拥挤状况，区政府对通往景区的道路进行了改造．某施工队承包道路改造任务共3300米，为了减少施工对周边居民及交通的影响，施工队加快了速度，比原计划每天多改造10%，结果提前3天完成了任务，求原计划每天改造道路多少米？

查看试题解析
26. 如图，一次函数y=kx+b与反比例函数y= $\frac{6}{x}$ （x＞0）的图象交于A（m，6），B（3，n）两点．

(1)、直接写出m= ， n=；

(2)、根据图象直接写出使kx+b＜ $\frac{6}{x}$ 成立的x的取值范围；

(3)、在x轴上找一点P使PA+PB的值最小，求出P点的坐标．

查看试题解析
27. 心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB，BC分别为线段，CD为双曲线的一部分)．

(1)、开始上课后第5分钟时与第30分钟时相比较，何时学生的注意力更集中？

(2)、一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？

查看试题解析