广东省深圳市育才三中2017-2018学年八年级下学期数学第一次月考试卷

试卷更新日期：2018-04-10 类型：月考试卷

进入出卷网下载

一、选择题

1. 三角形中，到三个顶点距离相等的点是（　　）

A、三条高线的交点 B、三条中线的交点 C、三条角平分线的交点 D、三边垂直平分线的交点

查看试题解析
2. 等腰三角形一个外角等于110°，则底角为（）

A、70°或40° B、40°或55° C、55°或70° D、70°

查看试题解析
3. 等腰三角形一边长等于5，一边长等于9，则它的周长是（）

A、14 B、23 C、19 D、19或23

查看试题解析
4. 如图，在△ABC中，AB=AC，点D，E分别在边BC和AC上，若AD=AE，则下列结论错误的是（）

A、∠ADB=∠ACB+∠CAD B、∠ADE=∠AED C、∠B=∠C D、∠BAD=∠BDA

查看试题解析
5. 如图，已知正比例函数y₁=ax与一次函数y₂= $\frac{1}{2}$ x+b的图象交于点P．下面有四个结论：①a＜0； ②b＜0； ③当x＞0时，y₁＞0；④当x＜﹣2时，y₁＞y₂ ．其中正确的是（）

A、①② B、②③ C、①③ D、①④

查看试题解析
6. 不等式﹣2x+6＞0的正整数解有（）

A、无数个 B、0个 C、1个 D、2个

查看试题解析
7. 一次函数y₁=kx+b与y₂=mx+n的部分自变量和对应函数值如下表：
x
…
0
1
2
3
…
y₁
…
2
$\frac{3}{2}$
1
$\frac{1}{2}$
…
x
…
0
1
2
3
…
y₂
…
﹣3
﹣1
1
3
…
则关于x的不等式kx+b＞mx+n的解集是（）

A、x＞2 B、x＜2 C、x＞1 D、x＜1

查看试题解析
8. 不等式x﹣1＞0 的解在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
9. 已知关于x的不等式组 ${\begin{matrix} 2 a + 3 x > 0 \\ 3 a - 2 x \geq 0 \end{matrix}$ 恰有3个整数解，则a的取值范围是（）

A、 $\frac{2}{3} \leq a \leq \frac{3}{2}$ B、 $\frac{4}{3} \leq a \leq \frac{3}{2}$ C、 $\frac{4}{3} < a \leq \frac{3}{2}$ D、 $\frac{4}{3} \leq a < \frac{3}{2}$

查看试题解析
10. 如图，在4×4方格中，以AB为一边，第三个顶点也在格点上的等腰三角形可以作出（）

A、7个 B、6个 C、4个 D、3个

查看试题解析
11. 在等边△ABC所在平面内找出一个点，使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形．这样的点一共有（）

A、1个 B、4个 C、7个 D、10个

查看试题解析
12. 如图，Rt△ACB中，∠ACB=90°，∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P，分别交AC和BC的延长线于E，D．过P作PF⊥AD交AC的延长线于点H，交BC的延长线于点F，连接AF交DH于点G．则下列结论：①∠APB=45°；②PF=PA；③BD﹣AH=AB；④DG=AP+GH．其中正确的是（）

A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析

二、填空题

13. 如图，下列4个三角形中，均有AB=AC，则经过三角形的一个顶点的一条直线不能够将这个三角形分成两个小等腰三角形的是（填序号）．

查看试题解析
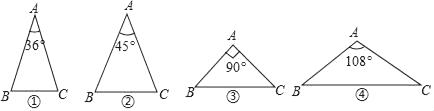14. 一等腰三角形一个外角是110°，则它的底角的度数为

查看试题解析
15. 不等式组 ${\begin{matrix} - 2 x < 6 \\ 3 (x - 2) \leq x - 4 \end{matrix}$ 的解集是．

查看试题解析
16. 如图，平面直角坐标系中，经过点B（﹣4，0）的直线y=kx+b与直线y=mx+2相交于点A $(- \frac{3}{2} ， - 1)$ ，则不等式mx+2＜kx+b＜0的解集为．

查看试题解析

三、解答题

17. 如图，在△ABC中，∠BAC=90°，AB=AC，点D在BC上，且BD=BA，点E在BC的延长线上，且CE=CA．

(1)、试求∠DAE的度数．

(2)、如果把原题中“AB=AC”的条件去掉，其余条件不变，那么∠DAE的度数会改变吗？为什么？

查看试题解析
18. 如图，在△ABC中，∠ABC的平分线与∠ACB的外角的平分线相交于点P，连接AP．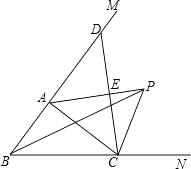

(1)、求证：PA平分∠BAC的外角∠CAM；

(2)、过点C作CE⊥AP，E是垂足，并延长CE交BM于点D．求证：CE=ED．

查看试题解析
19. 如图，AB∥CD，点E、N在AB上，点F在CD上，∠EFD的平分线FM交AB于点G，且GM=GN，若∠EFD=68°，求∠M的度数．

查看试题解析
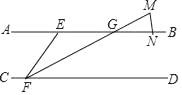20. 已知直线y=﹣2x+b经过点（1，1），求关于x的不等式﹣2x+b≥0的解集．

查看试题解析
21. 已知关于x的方程 $\frac{5 x + m}{3}$ ﹣ $\frac{x - 1}{2}$ =m的解为非负数，求m的取值范围．

查看试题解析
22. 解答题

(1)、解不等式 $\frac{x - 2}{2}$ ≤ $\frac{7 - x}{3}$ ．

(2)、解不等式组 ${\begin{matrix} x - 3 (x - 2) \geq 4 \\ \frac{2 x - 1}{5} < \frac{x + 1}{2} \end{matrix}$ 并将它的解集在数轴上表示出来．

查看试题解析
23. 某工厂接受了20天内生产1200台GH型电子产品的总任务．已知每台GH型产品由4个G型装置和3个H型装置配套组成．工厂现有80名工人，每个工人每天能加工6个G型装置或3个H型装置．工厂将所有工人分成两组同时开始加工，每组分别加工一种装置，并要求每天加工的G、H型装置数量正好全部配套组成GH型产品．

(1)、按照这样的生产方式，工厂每天能配套组成多少套GH型电子产品？请列出二元一次方程组解答此问题．

(2)、为了在规定期限内完成总任务，工厂决定补充一些新工人，这些新工人只能独立进行G型装置的加工，且每人每天只能加工4个G型装置．
①设原来每天安排x名工人生产G型装置，后来补充m名新工人，求x的值（用含m的代数式表示）
②请问至少需要补充多少名新工人才能在规定期内完成总任务？

查看试题解析

x	…	0	1	2	3	…
y₁	…	2	$\frac{3}{2}$	1	$\frac{1}{2}$	…

x	…	0	1	2	3	…
y₂	…	﹣3	﹣1	1	3	…