广东省五校协作体2017-2018学年高三文数第一次联考试卷试卷（1月份）

试卷更新日期：2018-04-10 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - 3 x + 2 = 0}, B = {x | x 〉 1}$ ,则 $A \cap C_{R} B =$ （）

A、 ${- 1}$ B、 ${1}$ C、 ${1, 2}$ D、 ${- 1, - 2}$

查看试题解析
2. 已知 $i$ 是虚数单位，复数 $z$ 满足 $(i - 1) z = i$ ，则 $z$ 的虚部是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2} i$ C、 $\frac{1}{2} i$ D、 $- \frac{1}{2}$

查看试题解析
3. “ $x > 1$ ”是“ ${log}_{2} (x + 1) > 1$ ” 的（）

A、充要条件 B、充分而不必要条件 C、必要而不充分条件 D、既不充分也不必要条件

查看试题解析
4. 函数 $f (x) = sin x cos x + (1 + {tan}^{2} x) {cos}^{2} x$ 的最小正周期和最大值分别是（）

A、 $π$ 和 $\frac{3}{2}$ B、 $\frac{π}{2}$ 和 $1$ C、 $π$ 和 $1$ D、 $2 π$ 和 $\frac{3}{2}$

查看试题解析
5. 已知 $M$ 是抛物线 $C : y^{2} = 2 p x (p > 0)$ 上一点， $F$ 是抛物线 $C$ 的焦点，若 $| M F | = p$ ， $k$ 是抛物线 $C$ 的准线与 $x$ 轴的交点，则 $∠ M K F =$ （）

A、45° B、30° C、15° D、60°

查看试题解析
6. 已知 $f (x) = sin x + \sqrt{3} cos x (x \in R)$ ，函数 $y = f (x + φ)$ 的图象关于直线 $x = 0$ 对称，则 $φ$ 的值可以是（）

A、 $\frac{π}{2}$ B、 $\frac{π}{3}$ C、 $\frac{π}{4}$ D、 $\frac{π}{6}$

查看试题解析
7. 函数 $f (x) = x^{2} ln x$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
8. 若函数 $f (x) = 2^{x}$ ， $g (x) = {(\frac{1}{3})}^{x}$ 则下列选项的命题为真命题的是（）

A、 $\forall x \in (- \infty, 0), f (x) > g (x)$ B、 $\forall x \in (- \infty, 0), f (x) < g (- x)$ C、 $\exists x \in (- \infty, 0), f (x) > g (- x)$ D、 $\exists x \in (- \infty, 0), f (- x) > g (x)$

查看试题解析
9. 一块硬质木料的三视图如图所示，正视图是边长为 $3 c m$ 的正方形，俯视图是 $3 c m \times 4 c m$ 的矩形，将该木料切削、打磨，加工成球，则能得到的最大球的半径最接近（）

A、1 cm B、2 cm C、3 cm D、4 cm

查看试题解析
10. 在区间 $[0 ， 2]$ 上任取两个数 $x, y$ 且 $x + y \leq 2$ ，则使 $x^{2} + y^{2} \leq 1$ 的概率是（）

A、 $\frac{π}{2}$ B、 $\frac{π}{4}$ C、 $\frac{π}{8}$ D、 $\frac{π}{16}$

查看试题解析
11. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ ，过其左焦点 $F$ 作 $x$ 轴的垂线，交双曲线于 $A, B$ 两点，若双曲线的右顶点在以 $A B$ 为直径的圆外，则双曲线离心率的取值范围是（）

A、 $(1, \frac{3}{2})$ B、 $(1, 2)$ C、 $(\frac{3}{2}, + \infty)$ D、 $(2, + \infty)$

查看试题解析
12. 某地为了调查去年上半年 $A$ 和 $B$ 两种农产品物价每月变化情况，选取数个交易市场统计数据进行分析，用 $a_{i}$ 和 $b_{i}$ 分别表示 $A$ 和 $B$ 两的当月单价均值（元 $/ k g$ ），下边流程图是对上述数据处理的一种算法（其中 $\bar{a} = 2 ， \bar{b} = 3$ ），则输出的值分别是（）
$i$
1月
2月
3月
4月
5月
6月
$a_{i}$
2.0
2.1
2.2
2.0
1.9
1.8
$b_{i}$
3.3
3.1
3.1
3.0
2.8
2.8

A、 $S = \frac{1}{60} ， T = \frac{1}{60}$ B、 $S = \frac{7}{30} ， T = \frac{1}{60}$ C、 $S = \frac{7}{30} ， T = \frac{7}{30}$ D、 $S = \frac{1}{60} ， T = \frac{7}{30}$

查看试题解析

二、填空题

13. 等差数列 ${a_{n}}$ 满足 $a_{2} + a_{8} = 6$ ，则 $a_{4} + a_{5} + a_{6} =$

查看试题解析
14. 已知 $\overset{⇀}{a} ， \overset{⇀}{b}$ 均为单位向量，它们的夹角为 $\frac{π}{3}$ ，则 $| \overset{⇀}{a} + \overset{⇀}{b} | =$

查看试题解析
15. 已知实数 $x ， y$ 满足 ${\begin{matrix} y \geq x + 2 \\ x + y \leq 6 \\ x \geq 1 \end{matrix}$ ，则 $z = 2 | x - 2 | + y$ 的最大值是．

查看试题解析
16. 已知 $a > 0$ ，函数 $f (x) = {\begin{matrix} s i n \frac{π}{2} x, x \in [- 1, 0) \\ a x^{2} + a x + 1, x \in [0, + \infty) \end{matrix}$ 若 $f (t - \frac{1}{3}) > - \frac{1}{2}$ ，则实数 $t$ 的取值范围为．

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $s_{n}$ ，且 $s_{n} = 2 a_{n} - 1$ ，

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、记 $b_{n} = \frac{a_{n}}{(a_{n} + 1) (a_{n + 1} + 1)}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 如图，四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是平行四边形， $∠ B A D = 60^{\circ}$ ，平面 $P A D ⊥$ 底面 $A B C D$ ，且 $Δ P A D$ 是边长为 $2$ 的等边三角形， $P B = \sqrt{6}$ ， $M$ 是 $A D$ 中点．

(1)、求证：平面 $P M B ⊥$ 平面 $P A D$ ；

(2)、证明： $∠ P D C > ∠ P A B$ ，且 $Δ P D C$ 与 $Δ P A B$ 的面积相等.

查看试题解析
19. 据某市地产数据研究院的数据显示，2016年该市新建住宅销售均价走势如图所示，为抑制房价过快上涨，政府从8月份采取宏观调控措施，10月份开始房价得到很好的抑制．
参考数据： $\sum_{i = 1}^{5} x_{i} = 25 ， \sum_{i = 1}^{5} y_{i} = 5.36 ， \sum_{i = 1}^{5} (x_{i} - \bar{x}) (y_{i} - \bar{y}) = 0.64$ ，（说明：以上数据 $x_{i} ， y_{i}$ 为3月至7月的数据）
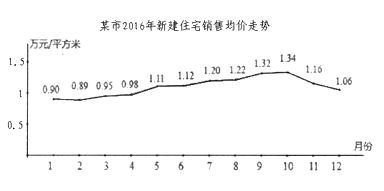
回归方程 $\overset{\land}{y} = \overset{\land}{b} x + \overset{\land}{a}$ 中斜率和截距的最小二乘估计公式分别为： $\overset{\land}{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\overset{\land}{a} = \bar{y} - \overset{\land}{b} \bar{x}$

(1)、地产数据研究院研究发现，3月至7月的各月均价 $y$ （万元/平方米）与月份 $x$ 之间具有较强的线性相关关系，试建立 $y$ 关于 $x$ 的回归方程（系数精确到 0.01），政府若不调控，依次相关关系预测第12月份该市新建住宅销售均价；

(2)、地产数据研究院在2016年的12个月份中，随机抽取三个月份的数据作样本分析，若关注所抽三个月份的所属季度，记不同季度的个数为X，求X的分布列和数学期望．

查看试题解析
20. 已知椭圆 $E : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点 $F_{1}$ 与抛物线 $y^{2} = - 4 x$ 的焦点重合，椭圆 $E$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，过点 $M (m, 0) (m > \frac{3}{4})$ 作斜率不为0的直线 $l$ ，交椭圆 $E$ 于 $A, B$ 两点，点 $P (\frac{5}{4}, 0)$ ，且 $\overset{⇀}{P A} • \overset{⇀}{P B}$ 为定值．

(1)、求椭圆 $E$ 的方程；

(2)、求 $Δ O A B$ 面积的最大值．

查看试题解析
21. 已知函数 $g (x) = \frac{a x + ln x}{x}$ ，（其中 $a$ 为常数）， $f (x) = x \cdot g (x)$ ．

(1)、求 $g (x)$ 的最大值；

(2)、若 $f (x)$ 在区间 $(0 ， e]$ 上的最大值为 $- 3$ ，求 $a$ 的值；

查看试题解析
22. 选修4-4：坐标系与参数方程
在直角坐标系 $x o y$ 中，直线 $l$ 的参数方程为 ${\begin{matrix} x = 3 - \frac{\sqrt{2}}{2} t \\ y = 4 + \frac{\sqrt{2}}{2} t \end{matrix}$ （ $t$ 为参数），在以原点 $O$ 为极点， $x$ 轴正半轴为极轴的极坐标系中，圆 $C$ 的方程为 $ρ = 6 sin θ$ ．

(1)、写出直线 $l$ 的普通方程和圆 $C$ 的直角坐标方程；

(2)、设点 $P (3 ， 4)$ ，直线 $l$ 与圆 $C$ 相交于 $A ， B$ 两点，求 $\frac{1}{| P A |} + \frac{1}{| P B |}$ 的值．

查看试题解析
23. 已知函数 $f (x) = | x - 2 | + | 2 x + 1 |$ ．

(1)、解不等式 $f (x) > 5$ ；

(2)、若关于 $x$ 的方程 $\frac{1}{f (x) - 4} = a$ 的解集为空集，求实数 $a$ 的取值范围．

查看试题解析

$i$	1月	2月	3月	4月	5月	6月
$a_{i}$	2.0	2.1	2.2	2.0	1.9	1.8
$b_{i}$	3.3	3.1	3.1	3.0	2.8	2.8