陕西省榆林市2018届理数高考第一次模拟考试
试卷更新日期:2018-04-09 类型:高考模拟
一、单选题
-
1. 设集合 ,集合 ,则 等于( )A、 B、 C、 D、2. 若向量 ,满足 ,则 ( )A、 B、 C、 D、3. 设Sn是等差数列{an}的前n项和,已知a2=3,a6=11,则S7等于( )A、13 B、35 C、49 D、634. 按下面的流程图进行计算.若输出的 ,则输出的正实数 值的个数最多为( )
 A、 B、 C、 D、5. 设 分别是椭圆 的左、右焦点,点 在椭圆 上,线段 的中点在 轴上,若 ,则椭圆的离心率为( )A、 B、 C、 D、6. 已知曲线 ,则下列说法正确的是( )A、把 上各点横坐标伸长到原来的 倍,再把得到的曲线向右平移 ,得到曲线 B、把 上各点横坐标伸长到原来的 倍,再把得到的曲线向右平移 ,得到曲线 C、把 向右平移 ,再把得到的曲线上各点横坐标缩短到原来的 ,得到曲线 D、把 向右平移 ,再把得到的曲线上各点横坐标缩短到原来的 ,得到曲线7. 《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何. 刍甍:底面为矩形的屋脊状的几何体(网络纸中粗线部分为其三视图,设网络纸上每个小正方形的边长为 丈),那么该刍甍的体积为( )
A、 B、 C、 D、5. 设 分别是椭圆 的左、右焦点,点 在椭圆 上,线段 的中点在 轴上,若 ,则椭圆的离心率为( )A、 B、 C、 D、6. 已知曲线 ,则下列说法正确的是( )A、把 上各点横坐标伸长到原来的 倍,再把得到的曲线向右平移 ,得到曲线 B、把 上各点横坐标伸长到原来的 倍,再把得到的曲线向右平移 ,得到曲线 C、把 向右平移 ,再把得到的曲线上各点横坐标缩短到原来的 ,得到曲线 D、把 向右平移 ,再把得到的曲线上各点横坐标缩短到原来的 ,得到曲线7. 《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何. 刍甍:底面为矩形的屋脊状的几何体(网络纸中粗线部分为其三视图,设网络纸上每个小正方形的边长为 丈),那么该刍甍的体积为( )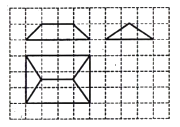 A、 立方丈 B、 立方丈 C、 立方丈 D、 立方丈8. 曲线 上一动点 处的切线斜率的最小值为( )A、 B、 C、 D、9. 已知直三棱柱 的 个顶点都在球 的球面上,若 ,则球 的直径为( )A、 B、 C、 D、10. 设 满足约束条件 ,若目标函数 的取值范围 恰好是函数 的一个单调递增区间,则 的值为( )A、 B、 C、 D、11. 已知 是双曲线 的左右两个焦点,过点 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点 ,若点 在以线段 为直径的圆外,则该双曲线离心率的取值范围是( )A、 B、 C、 D、12. 对于函数 和 ,设 , ,若存在 ,使得 ,则称 和 互为“零点相邻函数”,若函数 与 互为“零点相邻函数”,则实数 的取值范围是( )
A、 立方丈 B、 立方丈 C、 立方丈 D、 立方丈8. 曲线 上一动点 处的切线斜率的最小值为( )A、 B、 C、 D、9. 已知直三棱柱 的 个顶点都在球 的球面上,若 ,则球 的直径为( )A、 B、 C、 D、10. 设 满足约束条件 ,若目标函数 的取值范围 恰好是函数 的一个单调递增区间,则 的值为( )A、 B、 C、 D、11. 已知 是双曲线 的左右两个焦点,过点 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点 ,若点 在以线段 为直径的圆外,则该双曲线离心率的取值范围是( )A、 B、 C、 D、12. 对于函数 和 ,设 , ,若存在 ,使得 ,则称 和 互为“零点相邻函数”,若函数 与 互为“零点相邻函数”,则实数 的取值范围是( )
A、 B、 C、 D、二、填空题
-
13. 若角 的终边经过点 ,则 的值是 .
14. 有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说“是乙或丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了”.丁说:“是乙获奖.”四位歌手的话只有两句是对的,则获奖的歌手是 .15. 设 是不同的直线, 是不同的平面,则下列命题正确的是 .①若 ,则 或 .
②若 ,则 或 .
③若 ,则 或 与 相交.
④若 ,则 或 .
16. 在平面直角坐标系 中,已知点 是函数 的图象上的动点,该图象 在处的切线 交 轴于 点,过点 作 的垂线交 轴于点 ,设线段 的中点的纵坐标为 ,则 的最大值是 .三、解答题
-
17. 在 中,角 所对的边分别为 ,已知 .(1)、求角 的大小;(2)、若 ,求 的面积 的最大值.18. 数列 满足 .(1)、证明:数列 是等差数列;(2)、若 ,求 .19. 在如图所示的几何体中,四边形 为平行四边形, 平面 ,且 是 的中点.
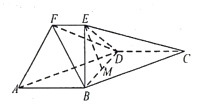 (1)、求证: 平面 ;(2)、求二面角 的余弦值的大小.20. 已知抛物线 的准线与 轴交于点 ,过点 做圆 的两条切线,切点为 .
(1)、求证: 平面 ;(2)、求二面角 的余弦值的大小.20. 已知抛物线 的准线与 轴交于点 ,过点 做圆 的两条切线,切点为 .
(1)、求抛物线 的方程;(2)、若直线 是讲过定点 的一条直线,且与抛物线 交于 两点,过定点 作 的垂线与抛物线交于 两点,求四边形 面积的最小值.21. 已知函数 ,记 .
(1)、求证: 在区间 内有且仅有一个实数;(2)、用 表示 中的最小值,设函数 ,若方程 在区间 内有两个不相等的实根 ,记 在 内的实根为 .求证: .