备考2018年中考数学一轮基础复习：专题二十二 圆的有关计算
试卷更新日期：2018-04-09 类型：一轮复习
一、单选题
-
1. “赶陀螺”是一项深受人们喜爱的运动，如图所示是一个陀螺的立体结构图，已知底面圆的直径AB=8cm，圆柱体部分的高BC=6cm，圆锥体部分的高CD=3cm，则这个陀螺的表面积是（ ）
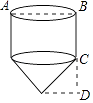A、68πcm2 B、74πcm2 C、84πcm2 D、100πcm22. 如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S1、S2、S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S4、S5、S6 ． 其中S1=16，S2=45，S5=11，S6=14，则S3+S4=（ ）
A、86 B、64 C、54 D、483. 用圆心角为120°，半径为3 cm的扇形纸片卷成一个圆锥形无底纸冒（如图所示），则这个纸冒的高是（ ）
A、3 cm B、2 cm C、3 cm D、4 cm4.如图，点A（2，0），B（0，2），将扇形AOB沿x轴正方向做无滑动的滚动，在滚动过程中点O的对应点依次记为点O1 ， 点O2 ， 点O3…，则O10的坐标是（ ）
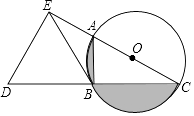
A、（16+4π，0） B、（14+4π，2） C、（14+3π，2） D、（12+3π，0）5. 如图，在△ABC中，AB=AC，∠ABC=45°，以AB为直径的⊙O交BC于点D，若BC=4 ，则图中阴影部分的面积为（ ）
A、π+1 B、π+2 C、2π+2 D、4π+16. 一个扇形的弧长是10πcm，面积是60πcm2 ， 则此扇形的圆心角的度数是（ ）A、300° B、150° C、120° D、75°7. 圆锥的底面半径r=3，高h=4，则圆锥的侧面积是（ ）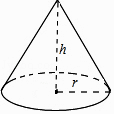
A、12π B、15π C、24π D、30π8. 如图，在Rt△ABC中，AC=5cm，BC=12cm，∠ACB=90°，把Rt△ABC所在的直线旋转一周得到一个几何体，则这个几何体的侧面积为（ ）
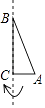A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm29. 如图，阴影部分是两个半径为1的扇形，若α=120°，β=60°，则大扇形与小扇形的面积之差为（ ）
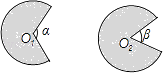A、 B、 C、 D、10. 手机上常见的wifi标志如图所示，它由若干条圆心相同的圆弧组成，其圆心角为90°，最小的扇形半径为1，若每两个相邻圆弧的半径之差为1，由里往外的阴影部分的面积依次记为S1、S2、S3…，则S1+S2+S3+…+S20= ．
11. 如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE，点B经过的路径为 ，则图中阴影部分的面积是（ ）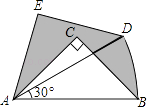
A、 B、 C、 ﹣ D、12.如图，在Rt△ABC中，∠A＝90°，BC＝ ．以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点，则 的长为 （ ）
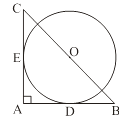A、 B、 C、 D、13. 如图，正五边形ABCDE内接于⊙O，若⊙O的半径为5，则 的长度为（ ）
A、π B、2π C、5π D、10π14. 正如我们小学学过的圆锥体积公式V= πr2h（π表示圆周率，r表示圆锥的底面半径，h表示圆锥的高）一样，许多几何量的计算都要用到π．祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家，创造了当时世界上的最高水平，差不多过了1000年，才有人把π计算得更精确．在辉煌成就的背后，我们来看看祖冲之付出了多少．现在的研究表明，仅仅就计算来讲，他至少要对9位数字反复进行130次以上的各种运算，包括开方在内．即使今天我们用纸笔来算，也绝不是一件轻松的事情，何况那时候没有现在的纸笔，数学计算不是用现在的阿拉伯数字，而是用算筹（小竹棍或小竹片）进行的，这需要怎样的细心和毅力啊！他这种严谨治学的态度，不怕复杂计算的毅力，值得我们学习．下面我们就来通过计算解决问题：已知圆锥的侧面展开图是个半圆，若该圆锥的体积等于9 π，则这个圆锥的高等于（ ）
A、 B、 C、 D、15.运用图形变化的方法研究下列问题：如图，AB是⊙O的直径，CD，EF是⊙O的弦，且AB∥CD∥EF，AB=10，CD=6，EF=8。则图中阴影部分的面积是（ ）
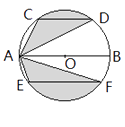A、 B、 C、 D、二、填空题
-
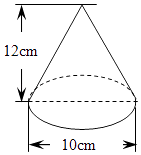
16. 圆锥的底面周长为6πcm，高为4cm，则该圆锥的全面积是；侧面展开扇形的圆心角是 ．17. 已知：如图，圆锥的底面直径是10cm，高为12cm，则它的侧面展开图的面积是cm2 ．
18. 如图，分别以正五边形ABCDE的顶点A，D为圆心，以AB长为半径画 ， ．若AB=1，则阴影部分图形的周长为（结果保留π）．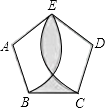
19. 如图，则△ABC中，∠BAC=100°，AB=AC=4，以点B为圆心，BA长为半径作圆弧，交BC于点D，则 的长为 ． （结果保留π）
20. 如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交 于点D，点F是 上一点．若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为 ．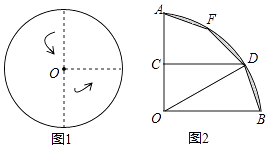
21.如图，在平面直角坐标系中，直线l的函数表达式为y=x，点O1的坐标为（1，0），以O1为圆心，O1O为半径画圆，交直线l于点P1 ， 交x轴正半轴于点O2 ， 以O2为圆心，O2O为半径画圆，交直线l于点P2 ， 交x轴正半轴于点O3 ， 以O3为圆心，O3O为半径画圆，交直线l于点P3 ， 交x轴正半轴于点O4；…按此做法进行下去，其中 的长为 ．
三、综合题
-
22.
如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（﹣3，4），B（﹣5，2），C（﹣2，1）．
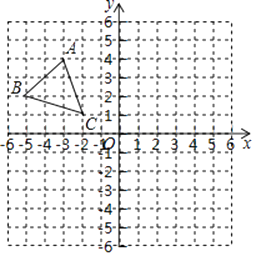(1)、画出△ABC关于y轴对称图形△A1B1C1；(2)、画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2；(3)、求（2）中线段OA扫过的图形面积．23. 如图，已知直线PT与⊙O相切于点T，直线PO与⊙O相交于A，B两点．
(1)、求证：PT2=PA•PB；(2)、若PT=TB= ，求图中阴影部分的面积．
