备考2018年中考数学一轮基础复习:专题二十一 与圆有关的位置关系
试卷更新日期:2018-04-09 类型:一轮复习
一、单选题
-
1. 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
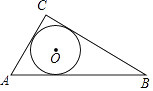 A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点2. 如图,已知直线AD是⊙O的切线,点A为切点,OD交⊙O于点B,点C在⊙O上,且∠ODA=36°,则∠ACB的度数为( )
A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点2. 如图,已知直线AD是⊙O的切线,点A为切点,OD交⊙O于点B,点C在⊙O上,且∠ODA=36°,则∠ACB的度数为( )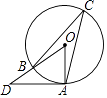 A、54° B、36° C、30° D、27°3. 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A、54° B、36° C、30° D、27°3. 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )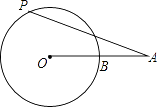 A、30° B、45° C、60° D、90°4. 如图为平面上圆O与四条直线l1、l2、l3、l4的位置关系.若圆O的半径为20公分,且O点到其中一直线的距离为14公分,则此直线为何?( )
A、30° B、45° C、60° D、90°4. 如图为平面上圆O与四条直线l1、l2、l3、l4的位置关系.若圆O的半径为20公分,且O点到其中一直线的距离为14公分,则此直线为何?( )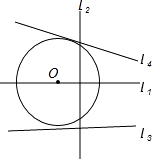 A、l1 B、l2 C、l3 D、l45. 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
A、l1 B、l2 C、l3 D、l45. 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( ) A、240° B、360° C、480° D、540°6. 如图,Rt△ABC中,∠C=90°,AC=4,BC=4 ,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
A、240° B、360° C、480° D、540°6. 如图,Rt△ABC中,∠C=90°,AC=4,BC=4 ,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )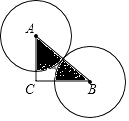 A、2π B、4π C、6π D、8π7. 已知,一元二次方程x2﹣8x+15=0的两根分别是⊙O1和⊙O2的半径,当⊙O1和⊙O2相切时,O1O2的长度是( )A、2 B、8 C、2或8 D、2<O1O2<88. 如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
A、2π B、4π C、6π D、8π7. 已知,一元二次方程x2﹣8x+15=0的两根分别是⊙O1和⊙O2的半径,当⊙O1和⊙O2相切时,O1O2的长度是( )A、2 B、8 C、2或8 D、2<O1O2<88. 如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:①AM=AD+MC;②AM=DE+BM;③DE2=AD•CM;④点N为△ABM的外心.其中正确的个数为( )
 A、1个 B、2个 C、3个 D、4个9. 如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
A、1个 B、2个 C、3个 D、4个9. 如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )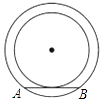 A、6cm B、4cm C、3cm D、8cm10. 已知:点P到直线l的距离为3,以点P为圆心,r为半径画圆,如果圆上有且只有两点到直线L的距离均为2,则半径r的取值范围是( )A、r>1 B、r>2 C、2<r<2 D、1<r<511. 在△ABC中,AB=AC=6,cos∠B= ,以点B为圆心,AB为半径作圆B,以点C为圆心,半径长为13作圆C,圆B与圆C的位置关系是( )A、外切 B、相交 C、内切 D、内含12. 如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
A、6cm B、4cm C、3cm D、8cm10. 已知:点P到直线l的距离为3,以点P为圆心,r为半径画圆,如果圆上有且只有两点到直线L的距离均为2,则半径r的取值范围是( )A、r>1 B、r>2 C、2<r<2 D、1<r<511. 在△ABC中,AB=AC=6,cos∠B= ,以点B为圆心,AB为半径作圆B,以点C为圆心,半径长为13作圆C,圆B与圆C的位置关系是( )A、外切 B、相交 C、内切 D、内含12. 如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( ) A、2 B、 ﹣ π C、1 D、 + π13. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
A、2 B、 ﹣ π C、1 D、 + π13. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )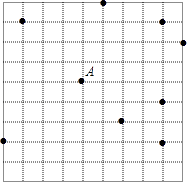 A、2 <r< B、 <r<3 C、 <r<5 D、5<r<14. 一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径是( )A、1.5cm B、7.5cm C、1.5cm或7.5cm D、3cm或15cm15. 如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依次A、B、C、D、E、F、C、G、A这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
A、2 <r< B、 <r<3 C、 <r<5 D、5<r<14. 一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径是( )A、1.5cm B、7.5cm C、1.5cm或7.5cm D、3cm或15cm15. 如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依次A、B、C、D、E、F、C、G、A这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( ) A、D点 B、E点 C、F点 D、G点
A、D点 B、E点 C、F点 D、G点二、填空题
-
16. 如图,已知Rt△ABC,∠C=90°,AC=3,BC=4.分别以点A、B为圆心画圆.如果点C在⊙A内,点B在⊙A外,且⊙B与⊙A内切,那么⊙B的半径长r的取值范围是 .
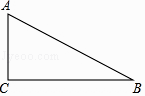 17. 如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为 .
17. 如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为 . 18. 在△ABC中,已知BC=4cm,以边AC的中点P为圆心1cm为半径画⊙P,以边AB的中点Q为圆心x cm长为半径画⊙Q,如果⊙P与⊙Q相切,那么x=cm.19. 如图,边长为4的正方形ABCD外切于⊙O,切点分别为E,F,G,H.则图中阴影部分的面积为 .
18. 在△ABC中,已知BC=4cm,以边AC的中点P为圆心1cm为半径画⊙P,以边AB的中点Q为圆心x cm长为半径画⊙Q,如果⊙P与⊙Q相切,那么x=cm.19. 如图,边长为4的正方形ABCD外切于⊙O,切点分别为E,F,G,H.则图中阴影部分的面积为 .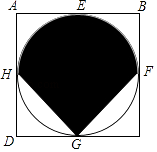 20. 如图,在平面直角坐标系xOy中,▱ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y= x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与▱ABCO的边相切时,P点的坐标为 .
20. 如图,在平面直角坐标系xOy中,▱ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y= x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与▱ABCO的边相切时,P点的坐标为 .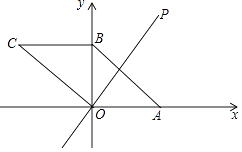 21.
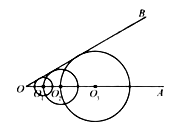
21.如图,已知 ,在射线 上取点 ,以 为圆心的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切; ;在射线 上取点 ,以 为圆心, 为半径的圆与 相切.若 的半径为 ,则 的半径长是 .
三、综合题
-
22. 如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
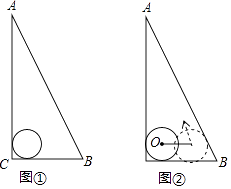 (1)、如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)(2)、如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.23. 如图,AB是⊙O的直径,BC是弦,过点O作OE⊥BC于H交⊙O于E,在OE的延长线上取一点D,使∠ODB=∠AEC,AE与BC交于F.
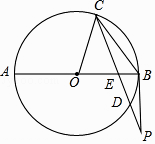
(1)、如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)(2)、如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.23. 如图,AB是⊙O的直径,BC是弦,过点O作OE⊥BC于H交⊙O于E,在OE的延长线上取一点D,使∠ODB=∠AEC,AE与BC交于F.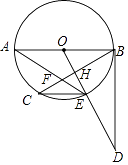 (1)、判断直线BD与⊙O的位置关系,并给出证明;(2)、当⊙O的半径是5,BF=2 ,EF= 时,求CE及BH的长.
(1)、判断直线BD与⊙O的位置关系,并给出证明;(2)、当⊙O的半径是5,BF=2 ,EF= 时,求CE及BH的长.