备考2018年中考数学一轮基础复习:专题十九 特殊的平行四边形
试卷更新日期:2018-04-09 类型:一轮复习
一、单选题
-
1. 如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
 A、3 B、10 C、9 D、92. 如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A、3 B、10 C、9 D、92. 如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )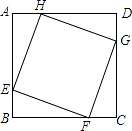 A、30 B、34 C、36 D、403. 求证:菱形的两条对角线互相垂直.
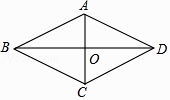
A、30 B、34 C、36 D、403. 求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )
 A、③→②→①→④ B、③→④→①→② C、①→②→④→③ D、①→④→③→②4. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3 ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
A、③→②→①→④ B、③→④→①→② C、①→②→④→③ D、①→④→③→②4. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3 ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( ) A、( , ) B、(2, ) C、( , ) D、( ,3﹣ )5. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A、( , ) B、(2, ) C、( , ) D、( ,3﹣ )5. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )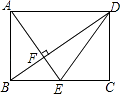 A、 B、 C、 D、6. 如图,在菱形 中, , , 是 的中点.过点 作 ,垂足为 .将 沿点 到点 的方向平移,得到 .设 、 分别是 、 的中点,当点 与点 重合时,四边形 的面积为( )
A、 B、 C、 D、6. 如图,在菱形 中, , , 是 的中点.过点 作 ,垂足为 .将 沿点 到点 的方向平移,得到 .设 、 分别是 、 的中点,当点 与点 重合时,四边形 的面积为( )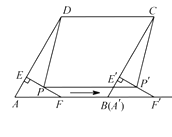 A、 B、 C、 D、7. 如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y= (x<0)的图象经过顶点B,则k的值为( )
A、 B、 C、 D、7. 如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y= (x<0)的图象经过顶点B,则k的值为( )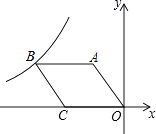 A、﹣12 B、﹣27 C、﹣32 D、﹣368. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连结DF,下列四个结论:①△AEF∽△CAB;②tan∠CAD= ;③DF=DC;④CF=2AF,正确的是( )
A、﹣12 B、﹣27 C、﹣32 D、﹣368. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连结DF,下列四个结论:①△AEF∽△CAB;②tan∠CAD= ;③DF=DC;④CF=2AF,正确的是( ) A、①②③ B、②③④ C、①③④ D、①②④9. 如图,菱形ABCD的边长为6,∠ABC=120°,M是BC边的一个三等分点,P是对角线AC上的动点,当PB+PM的值最小时,PM的长是( )
A、①②③ B、②③④ C、①③④ D、①②④9. 如图,菱形ABCD的边长为6,∠ABC=120°,M是BC边的一个三等分点,P是对角线AC上的动点,当PB+PM的值最小时,PM的长是( )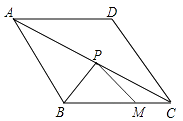 A、 B、 C、 D、10. 如图,在矩形ABCD中,AD=4,∠DAC=30°,点P、E分别在AC、AD上,则PE+PD的最小值是( )
A、 B、 C、 D、10. 如图,在矩形ABCD中,AD=4,∠DAC=30°,点P、E分别在AC、AD上,则PE+PD的最小值是( ) A、2 B、2 C、4 D、11. 如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
A、2 B、2 C、4 D、11. 如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )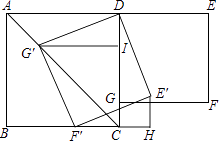 A、 B、 C、 D、12. 如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
A、 B、 C、 D、12. 如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )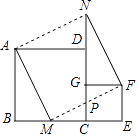 A、2 B、3 C、4 D、513. 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )
A、2 B、3 C、4 D、513. 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )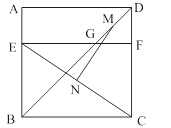 A、3 B、 C、 D、414. 如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 时,则 为( )
A、3 B、 C、 D、414. 如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 时,则 为( ) A、 B、2 C、 D、4
A、 B、2 C、 D、4二、填空题
-
15. 如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是 .
 16. 如图,正方形EFGH的顶点在边长为2的正方形的边上.若设AE=x,正方形EFGH的面积为y,则y与x的函数关系为 .
16. 如图,正方形EFGH的顶点在边长为2的正方形的边上.若设AE=x,正方形EFGH的面积为y,则y与x的函数关系为 . 17. 如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF= ,则CE= .
17. 如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF= ,则CE= . 18. 如图,已知菱形ABCD的周长为16,面积为8 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
18. 如图,已知菱形ABCD的周长为16,面积为8 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 . 19. 如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG=cm.
19. 如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG=cm.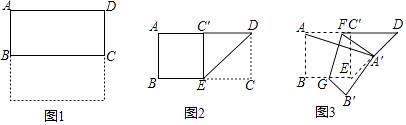 20. 如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则 的值为 .
20. 如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则 的值为 .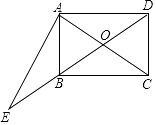
三、综合题
-
21. 在四边形ABCD中,对角线AC、BD交于点O.若四边形ABCD是正方形如图1:则有AC=BD,AC⊥BD.
旋转图1中的Rt△COD到图2所示的位置,AC′与BD′有什么关系?(直接写出)
若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC′与BD′又有什么关系?写出结论并证明.

 22.
22.如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 =n.
 (1)、求证:AE=GE;(2)、当点F落在AC上时,用含n的代数式表示 的值;(3)、若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.23. 如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.
(1)、求证:AE=GE;(2)、当点F落在AC上时,用含n的代数式表示 的值;(3)、若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.23. 如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.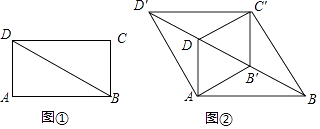 (1)、求证:四边形AB'C'D是菱形;(2)、四边形ABC'D′的周长为;(3)、将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.24. 如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A'落在∠ACB的外角平分线CD上,连结AA'.
(1)、求证:四边形AB'C'D是菱形;(2)、四边形ABC'D′的周长为;(3)、将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.24. 如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A'落在∠ACB的外角平分线CD上,连结AA'. (1)、判断四边形ACC'A'的形状,并说明理由;(2)、在△ABC中,∠B=90°,A B=24,cos∠BAC= ,求CB'的长.
(1)、判断四边形ACC'A'的形状,并说明理由;(2)、在△ABC中,∠B=90°,A B=24,cos∠BAC= ,求CB'的长.