备考2018年中考数学一轮基础复习:专题十八 多边形与平行四边形
试卷更新日期:2018-04-09 类型:一轮复习
一、单选题
-
1. 已知一个多边形的内角和是900°,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形2. 已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )A、8 B、9 C、10 D、113. 用正四边形和正八边形镶嵌成一个平面,则在某一个顶点处,正四边形和正八边形的个数分别为( )
A、2个和1个 B、1个和2个 C、3个和1个 D、1个和3个4. 一个多边形的内角和是外角和的2倍,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、八边形5. 如图,在▱ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( ) A、2 B、1 C、 D、6. 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y= (k>0,x>0)的图象经过点C,则k的值为( )
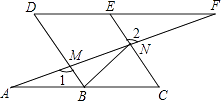
A、2 B、1 C、 D、6. 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y= (k>0,x>0)的图象经过点C,则k的值为( )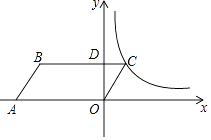 A、 B、 C、 D、7. 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
A、 B、 C、 D、7. 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( ) A、13 B、14 C、15 D、168. 如图,在▱ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① = ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A、13 B、14 C、15 D、168. 如图,在▱ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① = ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )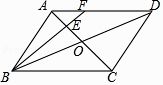 A、①②③④ B、①④ C、②③④ D、①②③9. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
A、①②③④ B、①④ C、②③④ D、①②③9. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( ) A、6 B、8 C、10 D、1210. 已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )A、∠BAC=∠DCA B、∠BAC=∠DAC C、∠BAC=∠ABD D、∠BAC=∠ADB11. 如图,▱ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB= ,AC=2,BD=4,则AE的长为( )
A、6 B、8 C、10 D、1210. 已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )A、∠BAC=∠DCA B、∠BAC=∠DAC C、∠BAC=∠ABD D、∠BAC=∠ADB11. 如图,▱ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB= ,AC=2,BD=4,则AE的长为( ) A、 B、 C、 D、12. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=8,AB=5,则AE的长为( )
A、 B、 C、 D、12. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=8,AB=5,则AE的长为( ) A、5 B、6 C、8 D、1213. 若正多边形的一个内角是150°,则该正多边形的边数是( )A、6 B、12 C、16 D、1814. 如图,E,F分别是▱ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
A、5 B、6 C、8 D、1213. 若正多边形的一个内角是150°,则该正多边形的边数是( )A、6 B、12 C、16 D、1814. 如图,E,F分别是▱ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( ) A、6 B、12 C、18 D、2415. 下列说法:
A、6 B、12 C、18 D、2415. 下列说法:①四边相等的四边形一定是菱形
②顺次连接矩形各边中点形成的四边形一定是正方形
③对角线相等的四边形一定是矩形
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有( )个.
A、4 B、3 C、2 D、1二、填空题
-
16. 如图,在▱ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S▱AEPH= .
 17. 如图,多边形ABCDE的每个内角都相等,则每个内角的度数为 .
17. 如图,多边形ABCDE的每个内角都相等,则每个内角的度数为 .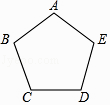 18. 在▱ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB= .19. 两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于度.
18. 在▱ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB= .19. 两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于度. 20. 如图所示的正六边形ABCDEF,连结FD,则∠FDC的大小为 .
20. 如图所示的正六边形ABCDEF,连结FD,则∠FDC的大小为 .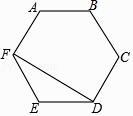 21. 如图,将▱ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=8,则AE的长为 .
21. 如图,将▱ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=8,则AE的长为 .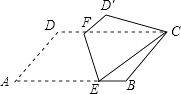
三、综合题
-
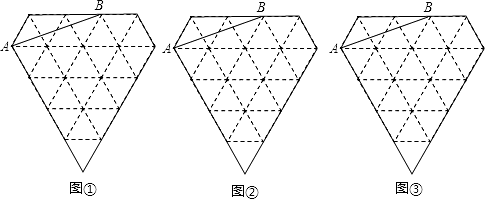
22. 如图,已知正七边形ABCDEFG,请仅用无刻度的直尺,分别按下列要求画图.
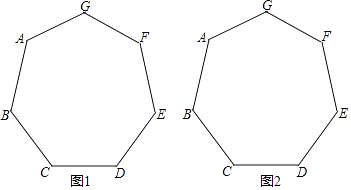 (1)、在图1中,画出一个以AB为边的平行四边形;(2)、在图2中,画出一个以AF为边的菱形.23. 在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.(1)、如果这个多边形是五边形,请求出这个外角的度数;(2)、是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.
(1)、在图1中,画出一个以AB为边的平行四边形;(2)、在图2中,画出一个以AF为边的菱形.23. 在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.(1)、如果这个多边形是五边形,请求出这个外角的度数;(2)、是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.