备考2018年中考数学一轮基础复习:专题十七 全等三角形
试卷更新日期:2018-04-09 类型:一轮复习
一、单选题
-
1. 如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长为( )
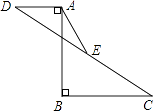 A、6 B、 C、5 D、2. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:
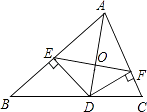
A、6 B、 C、5 D、2. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:①OA=OD;
②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.
其中一定正确的是( )
 A、①②③ B、②③④ C、①③④ D、①②③④3.
A、①②③ B、②③④ C、①③④ D、①②③④3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
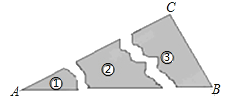 A、带①去 B、带②去 C、带③去 D、①②③都带去4. 如图,在△ABC中,D、E分别是AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是( )
A、带①去 B、带②去 C、带③去 D、①②③都带去4. 如图,在△ABC中,D、E分别是AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是( )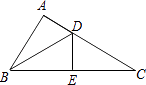 A、15° B、20° C、25° D、30°5.
A、15° B、20° C、25° D、30°5.如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤S△HCF=S△ADH ,
其中正确的结论有( )
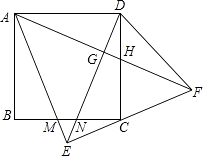 A、2个 B、3个 C、4个 D、5个6. 如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
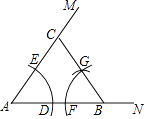
A、2个 B、3个 C、4个 D、5个6. 如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )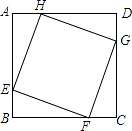 A、30 B、34 C、36 D、407. 如图,已知∠MAN=55°,点B为AN上一点.用尺规按如下过程作图:
A、30 B、34 C、36 D、407. 如图,已知∠MAN=55°,点B为AN上一点.用尺规按如下过程作图:以点A为圆心,以任意长为半径作弧,交AN于点D,交AM于点E;以点B为圆心,以AD为半径作弧,交AB于点F;以点F为圆心,以DE为半径作弧,交前面的弧于点G;连接BG并延长交AM于点C.则∠BCM的度数为( )
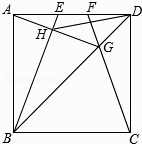
 A、70° B、110° C、125° D、130°8. 如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
A、70° B、110° C、125° D、130°8. 如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2 ﹣2.
 A、2 B、3 C、4 D、59. 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )
A、2 B、3 C、4 D、59. 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )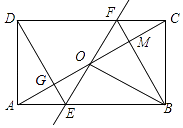 A、4个 B、3个 C、2个 D、1个10. 一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017D2017的边长是( )
A、4个 B、3个 C、2个 D、1个10. 一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017D2017的边长是( )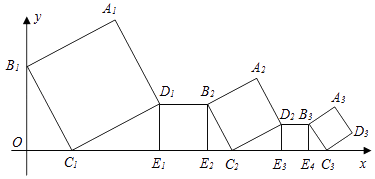 A、( )2016 B、( )2017 C、( )2016 D、( )201711. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、( )2016 B、( )2017 C、( )2016 D、( )201711. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )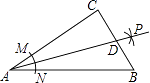 A、15 B、30 C、45 D、6012. 如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )
A、15 B、30 C、45 D、6012. 如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( ) A、 B、 C、 D、13.
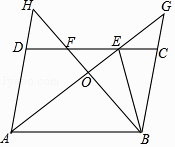
A、 B、 C、 D、13.如图,在▱ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
 A、BO=OH B、DF=CE C、DH=CG D、AB=AE14. 如图,对正方形纸片ABCD进行如下操作:
A、BO=OH B、DF=CE C、DH=CG D、AB=AE14. 如图,对正方形纸片ABCD进行如下操作: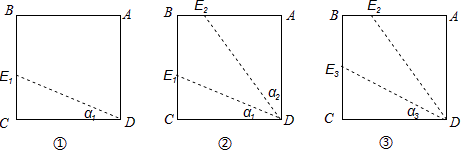
(i)过点D任作一条直线与BC边相交于点E1(如图①),记∠CDE1=α1;
(ii)作∠ADE1的平分线交AB边于点E2(如图②),记∠ADE2=α2;
(iii)作∠CDE2的平分线交BC边于点E3(如图③),记∠CDE3=α3;
按此作法从操作(2)起重复以上步骤,得到α1 , α2 , …,αn , …,现有如下结论:①当α1=10°时,α2=40°;②2α4+α3=90°; ③当α5=30°时,△CDE9≌△ADE10;④当α1=45°时,BE2= .
其中正确的个数为( )
A、1 B、2 C、3 D、415.如图,在矩形ABCD中,P是BC上一点,E是AB上一点,PD平分∠APC,PE⊥PD,连接DE交AP于F,在以下判断中,不正确的是( )
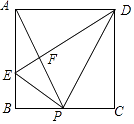 A、当P为BC中点,△APD是等边三角形 B、当△ADE∽△BPE时,P为BC中点 C、当AE=2BE时,AP⊥DE D、当△APD是等边三角形时,BE+CD=DE
A、当P为BC中点,△APD是等边三角形 B、当△ADE∽△BPE时,P为BC中点 C、当AE=2BE时,AP⊥DE D、当△APD是等边三角形时,BE+CD=DE二、填空题
-
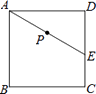
16.
如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于
 17. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,垂足为E点,请任意写出一组相等的线段 .
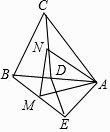
17. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,垂足为E点,请任意写出一组相等的线段 .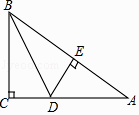 18. 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D在AB上,点E与点C在AB的两侧,连接BE,CD,点M、N分别是BE、CD的中点,连接MN,AM,AN.
18. 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D在AB上,点E与点C在AB的两侧,连接BE,CD,点M、N分别是BE、CD的中点,连接MN,AM,AN.下列结论:①△ACD≌△ABE;②△ABC∽△AMN;③△AMN是等边三角形;④若点D是AB的中点,则S△ABC=2S△ABE .
其中正确的结论是 . (填写所有正确结论的序号)
 19. 如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)
19. 如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)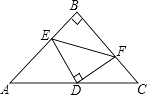 20.
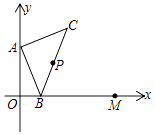
20.如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为 .
 21.
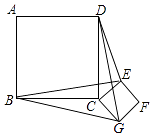
21.如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)
三、综合题
-
22. 已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB交AE的延长线于点F.
 (1)、求证:△ADE≌△FCE;(2)、若∠DCF=120°,DE=2,求BC的长.23.
(1)、求证:△ADE≌△FCE;(2)、若∠DCF=120°,DE=2,求BC的长.23.已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
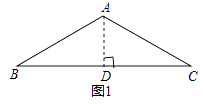
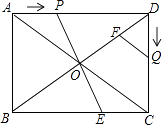 (1)、当t为何值时,AP=PO.(2)、设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.24. 问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD= ∠BAC=60°,于是 = = ;
(1)、当t为何值时,AP=PO.(2)、设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.24. 问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD= ∠BAC=60°,于是 = = ;迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.
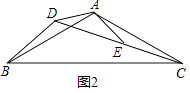 (1)、①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;(2)、拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(1)、①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;(2)、拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.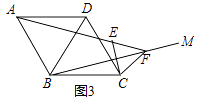
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.
25. △ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.(1)、观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)
 (2)、
(2)、数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
 (3)、
(3)、拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ,CD= BC,请求出GE的长.
