2015-2016学年浙江省杭州市余杭区高二上学期期末数学试卷

试卷更新日期：2016-11-30 类型：期末考试

进入出卷网下载

一、选择题

1. 在平面直角坐标系中，过（1，0）点且倾率为﹣1的直线不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知数列{a_n}是等差数列，若a₁﹣a₉+a₁₇=7，则a₃+a₁₅=（）

A、7 B、14 C、21 D、7（n﹣1）

查看试题解析
3. 圆（x+2）²+（y﹣3）²=5的圆心坐标、半径分别是（）

A、（2，﹣3）、5 B、（﹣2，3）、5 C、（﹣2，3）、 $\sqrt{5}$ D、（ 3，﹣2）、 $\sqrt{5}$

查看试题解析
4. 设a，b，c∈R，且a＞b，则（）

A、ac＞bc B、 $\frac{1}{a} ＜ \frac{1}{b}$ C、a²＞b² D、a³＞b³

查看试题解析
5. 若不论m取何实数，直线l：mx+y﹣1+2m=0恒过一定点，则该定点的坐标为（　　）

A、（﹣2，1） B、（2，﹣1） C、（﹣2，﹣1） D、（2，1）

查看试题解析
6. 如图，在正方体ABCD﹣A₁B₁C₁D₁中，E，F，G，H分别为AA₁ ， AB，BB₁ ， B₁C₁的中点，则异面直线EF与GH所成的角等于（）

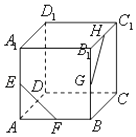A、45° B、60° C、90° D、120°

查看试题解析
7. 已知点A（2，3）、B（﹣5，2），若直线l过点P（﹣1，6），且与线段AB相交，则直线l斜率的取值范围是（）

A、[﹣1，1] B、（﹣∞，﹣1]∪[1，+∞） C、（﹣1，1） D、（﹣∞，﹣1）∪（1，+∞）

查看试题解析
8. 设a、b是不同的直线，α、β是不同的平面，则下列四个命题中正确的是（）

A、若a⊥b，a⊥α，则b∥α B、若a∥α，α⊥β，则a⊥β C、若a⊥β，α⊥β，则a∥α D、若a⊥b，a⊥α，b⊥β，则α⊥β

查看试题解析
9. 若变量x，y满足约束条件 ${\begin{matrix} x - y \geq 0 \\ x + y \leq 4 \\ y + k \geq 0 \end{matrix}$ 且z=3x+y的最小值为﹣8，则k=（）

A、2 B、﹣2 C、3 D、﹣3

查看试题解析
10. 不等式|x+3|﹣|x﹣1|≤2^a对任意实数x恒成立，则实数a的取值范围是（）

A、（﹣∞，﹣2] B、（﹣∞，﹣2]∪[2，+∞） C、[2，+∞） D、a∈R

查看试题解析
11. 若正实数a，b满足a+b=1，则（　　）

A、 $\frac{1}{a} + \frac{1}{b}$ 有最大值4 B、ab有最小值 $\frac{1}{4}$ C、 $\sqrt{a}$ + $\sqrt{b}$ 有最大值 $\sqrt{2}$ D、a²+b²有最小值 $\frac{\sqrt{2}}{2}$

查看试题解析
12. 已知直线x+y+m=0与圆x²+y²=4交于不同的两点A，B，O是坐标原点， $| \vec{O A} + \vec{O B} | \geq | \vec{A B} |$ ，则实数m的取值范围是（）

A、[﹣2，2] B、 $[2 ， 2 \sqrt{2}) \cup (- 2 ， - 2]$ C、 $(- 2 \sqrt{2} ， - 2]$ D、 $[2 ， 2 \sqrt{2})$

查看试题解析

二、填空题

13. 数列﹣1，4，﹣16，64，﹣256，…的一个通项公式a_n= ．

查看试题解析
14. 已知直线ax+y+2=0与直线x﹣（3a﹣1）y﹣1=0互相垂直，则a=

查看试题解析
15. 若2、a、b、c、9成等差数列，则c﹣a= ．

查看试题解析
16. 在圆x²+y²=5x内，过点 $(\frac{5}{2} ， \frac{3}{2})$ 有n条弦的长度成等差数列，最短弦长为数列的首项a₁ ，最长弦长为a_n ，若公差 $d \in (\frac{1}{6} ， \frac{1}{3}]$ ，那么n的取值集合．

查看试题解析
17. 如图是某几何体的三视图（单位：cm），则该几何体的表面积是 cm² ，体积为 cm³ ．

查看试题解析
18. 已知两矩形ABCD与ADEF所在的平面互相垂直，AB=1，若将△DEF沿直线FD翻折，使得点E落在边BC上（即点P），则当AD取最小值时，边AF的长是；此时四面体F﹣ADP的外接球的半径是．

查看试题解析

三、解答题

19. 已知函数f（x）=ax²﹣x+a，a∈R，

(1)、当a=2时，解不等式f（x）＞3；

(2)、若函数f（x）有最大值﹣2，求实数a的值．

查看试题解析
20. 已知圆C：x²+y²﹣6x﹣4y+4=0，点P（6，0）．

(1)、求过点P且与圆C相切的直线方程l；

(2)、若圆M与圆C外切，且与x轴切于点P，求圆M的方程．

查看试题解析
21. 如图，几何体ABCDE中，△ABC是正三角形，EA和DC都垂直于平面ABC，且EA=AB=2a，DC=a，F，G分别为EB和AB的中点．

(1)、求证：FD∥平面ABC；

(2)、求二面角B﹣FC﹣G的正切值．

查看试题解析
22. 已知数列{b_n}是首项b₁=1，b₄=10的等差数列，设b_n+2=3 $\log_{\frac{1}{4}}$ a_n（n∈n^*）．

(1)、求证：{a_n}是等比数列；

(2)、记c_n= $\frac{1}{b_{n} b_{n + 1}}$ ，求数列{c_n}的前n项和S_n；

(3)、记d_n=（3n+1）•S_n ，若对任意正整数n，不等式 $\frac{1}{n + d_{1}}$ + $\frac{1}{n + d_{2}}$ +…+ $\frac{1}{n + d_{n}}$ ＞ $\frac{m}{24}$ 恒成立，求整数m的最大值．

查看试题解析