备考2018年中考数学一轮基础复习：专题十六 等腰三角形与直角三角形
试卷更新日期：2018-04-09 类型：一轮复习
一、单选题
-
1. 如图是由8个全等的矩形组成的大正方形，线段AB的端点都在小矩形的顶点上，如果点P是某个小矩形的顶点，连接PA、PB，那么使△ABP为等腰直角三角形的点P的个数是（ ）
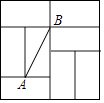A、2个 B、3个 C、4个 D、5个2. 如图，在△ABC中，AB=5，AC=4，BC=3，分别以点A，点B为圆心，大于 AB的长为半径画弧，两弧相交于点M，N，作直线MN交AB于点O，连接CO，则CO的长是（ ）
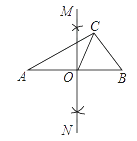A、1.5 B、2 C、2.4 D、2.53. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．若AC=3，AB=5，则CE的长为（ ）
A、 B、 C、 D、4. 若等腰三角形的周长为10cm，其中一边长为2cm，则该等腰三角形的底边长为（ ）A、2cm B、4cm C、6cm D、8cm5. 如图，在△ABC中，AB=AC，E，F分别是BC，AC的中点，以AC为斜边作Rt△ADC，若∠CAD=∠CAB=45°，则下列结论不正确的是（ ）
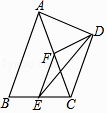A、∠ECD=112.5° B、DE平分∠FDC C、∠DEC=30° D、AB= CD6.如图，在△ABC中，中线BE，CD相交于点O，连接DE，下列结论：
① ；② ；③ ；④
其中正确的个数有（ ）
A、1个 B、2个 C、3个 D、4个7. 如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，点E是AB的中点，CD=DE=a，则AB的长为（ ）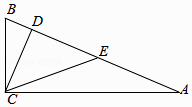
A、2a B、2 a C、3a D、8. 如图，在正方形ABCD中，点E，F分别在BC，CD上，且∠EAF=45°，将△ABE绕点A顺时针旋转90°，使点E落在点E'处，则下列判断不正确的是（ ）
A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形9. 已知等边△ABC的边长为12，D是AB上的动点，过D作DE⊥AC于点E，过E作EF⊥BC于点F，过F作FG⊥AB于点G．当G与D重合时，AD的长是（ ）A、3 B、4 C、8 D、910. 如图，在△ABC中，AB=AC，∠A=30°，AB的垂直平分线l交AC于点D，则∠CBD的度数为（ ）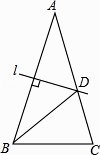
A、30° B、45° C、50° D、75°11.如图，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P是AD上一个动点，则下列线段的长度等于BP+EP最小值的是（ ）
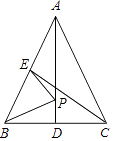A、BC B、CE C、AD D、AC12. 如图，在Rt△ABC中，∠ABC=90°，AB=6，BC=8，∠BAC，∠ACB的平分线相交于点E，过点E作EF∥BC交AC于点F，则EF的长为（ ）
A、 B、 C、 D、13. 如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（ ）
A、4 B、5 C、6 D、714. 如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交AD的延长线于点E．若AB=12，BM=5，则DE的长为（ ）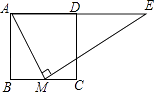
A、18 B、 C、 D、15. 如图，△ABC中，∠BAC=90°，AB=3，AC=4，点D是BC的中点，将△ABD沿AD翻折得到△AED，连CE，则线段CE的长等于（ ）
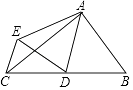A、2 B、 C、 D、二、填空题
-
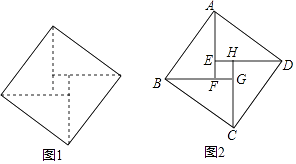
16. 如图1，这个图案是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．此图案的示意图如图2，其中四边形ABCD和四边形EFGH都是正方形，△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形．若EF=2，DE=8，则AB的长为 ．
17. 在等腰△ABC中，AD⊥BC交直线BC于点D，若AD= BC，则△ABC的顶角的度数为 ．18. 如图，在四边形ABCD中，∠ABC=∠ADC=90°，E为对角线AC的中点，连接BE，ED，BD．若∠BAD=58°，则∠EBD的度数为度．
19.我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是尺．
20. 在△ABC中，AB=6，点D是AB的中点，过点D作DE∥BC，交AC于点E，点M在DE上，且ME= DM．当AM⊥BM时，则BC的长为 ．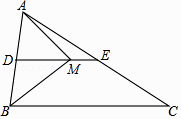
21. 如图，等边△A1C1C2的周长为1，作C1D1⊥A1C2于D1 ， 在C1C2的延长线上取点C3 ， 使D1C3=D1C1 ， 连接D1C3 ， 以C2C3为边作等边△A2C2C3；作C2D2⊥A2C3于D2 ， 在C2C3的延长线上取点C4 ， 使D2C4=D2C2 ， 连接D2C4 ， 以C3C4为边作等边△A3C3C4；…且点A1 ， A2 ， A3 ， …都在直线C1C2同侧，如此下去，则△A1C1C2 ， △A2C2C3 ， △A3C3C4 ， …，△AnCnCn+1的周长和为 ． （n≥2，且n为整数）
三、综合题
-
22. 在边长为2的等边三角形ABC中，P是BC边上任意一点，过点 P分别作 PM⊥A B，PN⊥AC，M、N分别为垂足．
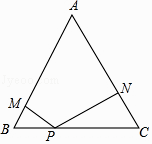(1)、求证：不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高；(2)、当BP的长为何值时，四边形AMPN的面积最大，并求出最大值．23. 如图，已知等腰三角形ABC中，AB=AC，点D、E分别在边AB、AC上，且AD=AE，连接BE、CD，交于点F．
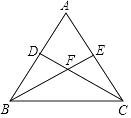(1)、判断∠ABE与∠ACD的数量关系，并说明理由；(2)、求证：过点A、F的直线垂直平分线段BC．24. 如图1，△ABC中，CD⊥AB于D，且BD：AD：CD=2：3：4，
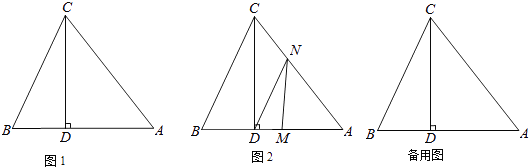(1)、试说明△ABC是等腰三角形；(2)、已知S△ABC=40cm2 ， 如图2，动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止．设点M运动的时间为t（秒），①若△DMN的边与BC平行，求t的值；
25. 在图1﹣﹣图4中，菱形ABCD的边长为3，∠A=60°，点M是AD边上一点，且DM= AD，点N是折线AB﹣BC上的一个动点．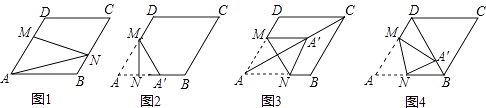
(1)、如图1，当N在BC边上，且MN过对角线AC与BD的交点时，则线段AN的长度为 ．(2)、当点N在AB边上时，将△AMN沿MN翻折得到△A′MN，如图2，①若点A′落在AB边上，则线段AN的长度为；
②当点A′落在对角线AC上时，如图3，求证：四边形AM A′N是菱形；
③当点A′落在对角线BD上时，如图4，求 的值．