备考2018年中考数学一轮基础复习:专题十五 图形的初步
试卷更新日期:2018-04-09 类型:一轮复习
一、单选题
-
1. 如图,下列图形全部属于柱体的是( )A、
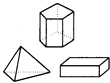 B、
B、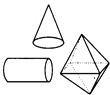 C、
C、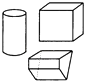 D、
D、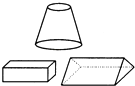 2. 如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( )
2. 如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为( ) A、54° B、62° C、64° D、74°3. 下列各图中,∠1与∠2互为邻补角的是( )A、
A、54° B、62° C、64° D、74°3. 下列各图中,∠1与∠2互为邻补角的是( )A、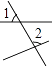 B、
B、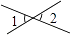 C、
C、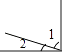 D、
D、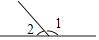 4. 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
4. 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )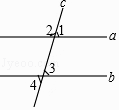 A、∠1=∠3 B、∠2+∠4=180° C、∠1=∠4 D、∠3=∠45. 如图所示,点P到直线l的距离是( )
A、∠1=∠3 B、∠2+∠4=180° C、∠1=∠4 D、∠3=∠45. 如图所示,点P到直线l的距离是( ) A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度6. 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )
A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度6. 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( ) A、∠BAO与∠CAO相等 B、∠BAC与∠ABD互补 C、∠BAO与∠ABO互余 D、∠ABO与∠DBO不等7. 把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度数为( )
A、∠BAO与∠CAO相等 B、∠BAC与∠ABD互补 C、∠BAO与∠ABO互余 D、∠ABO与∠DBO不等7. 把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度数为( ) A、115° B、120° C、145° D、135°8. 如图,直线l1∥l2∥l3 , 点A,B,C分别在直线l1、l2、l3上,若∠1=72°,∠2=48°,则∠ABC=( )
A、115° B、120° C、145° D、135°8. 如图,直线l1∥l2∥l3 , 点A,B,C分别在直线l1、l2、l3上,若∠1=72°,∠2=48°,则∠ABC=( )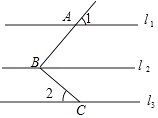 A、24° B、120° C、96° D、132°9. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
A、24° B、120° C、96° D、132°9. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )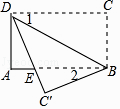 A、20° B、30° C、35° D、55°10.
A、20° B、30° C、35° D、55°10.如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
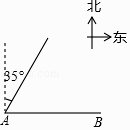 A、北偏东55° B、北偏西55° C、北偏东35° D、北偏西35°11. 小军将一个直角三角板(如图)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是( )
A、北偏东55° B、北偏西55° C、北偏东35° D、北偏西35°11. 小军将一个直角三角板(如图)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 12. 某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
12. 某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( ) A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、经过直线外一点,有且只有一条直线与这条直线平行13. 如图,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有( )
A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、经过直线外一点,有且只有一条直线与这条直线平行13. 如图,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有( ) A、4个 B、3个 C、2个 D、1个14. 如图,OP平分∠MON,PA⊥OA于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的值为( )
A、4个 B、3个 C、2个 D、1个14. 如图,OP平分∠MON,PA⊥OA于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的值为( ) A、1 B、2 C、大于2 D、不小于215. 过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其正确展开图为( )A、
A、1 B、2 C、大于2 D、不小于215. 过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其正确展开图为( )A、 B、
B、 C、
C、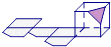 D、
D、
二、填空题
-
16. 如图,点D是线段AB的中点,点C是线段AD的中点,若CD=1,则AB= .
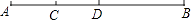 17. 如图,若∠1+∠2=180°,∠3=110°,则∠4= .
17. 如图,若∠1+∠2=180°,∠3=110°,则∠4= .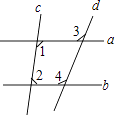 18.
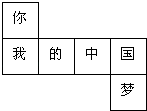
18.如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面相对面上的字是 .
 19. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=48°,则∠AED为°.
19. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=48°,则∠AED为°.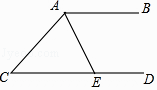 20. 一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是 .
20. 一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是 .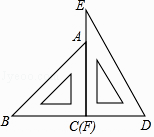 21. 如图,直线l1//l2 , ∠1=20°,则∠2+∠3= .
21. 如图,直线l1//l2 , ∠1=20°,则∠2+∠3= .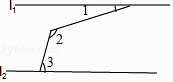
三、综合题
-
22. 尺规作图:(用圆规和直尺作图,不写过程,但要保留作图痕迹)
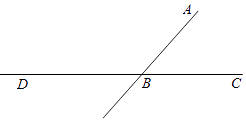
已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点.
求作:点E,使直线DE∥AB,且使线段BE长度最短.
 23. 定义:对于平面直角坐标系中的任意直线MN及点P,取直线MN上一点Q,线段PQ与直线MN成30°角的长度称为点P到直线MN的30°角的距离,记作d(P→MN).
23. 定义:对于平面直角坐标系中的任意直线MN及点P,取直线MN上一点Q,线段PQ与直线MN成30°角的长度称为点P到直线MN的30°角的距离,记作d(P→MN).已知O为坐标原点,A(4,0),B(3,3)是平面直角坐标系中两点.根据上述定义,解答下列问题:
 (1)、点A到直线OB的30°角的距离d(A→OB)=;(2)、已知点G到线段OB的30°角的距离d(G→OB)=2,且点G的横坐标为1,则点G的纵坐标为 .(3)、若点A到直线l:y=kx+1的30°角的距离d(A→l)=4,求k的值.24. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)、点A到直线OB的30°角的距离d(A→OB)=;(2)、已知点G到线段OB的30°角的距离d(G→OB)=2,且点G的横坐标为1,则点G的纵坐标为 .(3)、若点A到直线l:y=kx+1的30°角的距离d(A→l)=4,求k的值.24. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.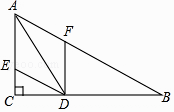 (1)、求AD的长;(2)、求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)25. 阅读下面材料:
(1)、求AD的长;(2)、求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)25. 阅读下面材料:实际问题:如图(1),一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.

解决方案:
路线1:侧面展开图中的线段AC,如图(2)所示,
设路线l的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2;
路线2:高线AB+底面直径BC,如图(1)所示.
设路线2的长度为l2:则l22=(AB+BC)2=(5+10)2=225.
为比较l1 , l2的大小,我们采用“作差法”:
∵l12﹣l22=25(π2﹣8)>0∴l12>l22∴l1>l2 ,
小明认为应选择路线2较短.
(1)、问题类比:小亮对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”.请你用上述方法帮小亮比较出l1与l2的大小:
(2)、问题拓展:请你帮他们继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,当 满足什么条件时,选择路线2最短?请说明理由.
(3)、问题解决:如图(3)为2个相同的圆柱紧密排列在一起,高为5厘米,当蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.(注:按上面小明所设计的两条路线方式).