备考2018年中考数学一轮基础复习：专题十四 二次函数的图象和性质
试卷更新日期：2018-04-09 类型：一轮复习
一、单选题
-
1. 下列函数中，是二次函数的有（ ）
①y=1﹣ x2②y= ③y=x（1﹣x）④y=（1﹣2x）（1+2x）
A、1个 B、2个 C、3个 D、4个2. 抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位，所得图象的解析式为y=x2﹣2x﹣3，则b、c的值为（ ）A、b=2，c=2 B、b=2，c=0 C、b=﹣2，c=﹣1 D、b=﹣3，c=23. 如图，抛物线y=x2﹣2x﹣3与y轴交于点C，点D的坐标为（0，﹣1），在第四象限抛物线上有一点P，若△PCD是以CD为底边的等腰三角形，则点P的横坐标为（ ）
A、1+ B、1﹣ C、 ﹣1 D、1﹣ 或1+4. 已知一次函数y1=4x，二次函数y2=2x2+2，在实数范围内，对于x的同一个值，这两个函数所对应的函数值为y1与y2 ， 则下列关系正确的是（ ）A、y1＞y2 B、y1≥y2 C、y1＜y2 D、y1≤y25.如图，在平面直角坐标系中2条直线为l1：y=﹣3x+3，l2：y=﹣3x+9，直线l1交x轴于点A，交y轴于点B，直线l2交x轴于点D，过点B作x轴的平行线交l2于点C，点A、E关于y轴对称，抛物线y=ax2+bx+c过E、B、C三点，下列判断中：
①a﹣b+c=0；②2a+b+c=5；③抛物线关于直线x=1对称；④抛物线过点（b，c）；⑤S四边形ABCD=5，
其中正确的个数有（ ）
A、5 B、4 C、3 D、26.已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则正比例函数y=（b+c）x与反比例函数y= 在同一坐标系中的大致图象是（ ）
A、
B、
C、
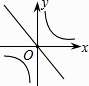D、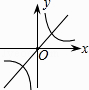
7. 已知抛物线y=ax2（a＞0）过A（﹣2，y1）、B（1，y2）两点，则下列关系式一定正确的是（ ）A、y1＞0＞y2 B、y2＞0＞y1 C、y1＞y2＞0 D、y2＞y1＞08. 如图，在△ABC中，∠C=90°，AB=10cm，BC=8cm，点P从点A沿AC向点C以1cm/s的速度运动，同时点Q从点C沿CB向点B以2cm/s的速度运动（点Q运动到点B停止），在运动过程中，四边形PABQ的面积最小值为（ ）
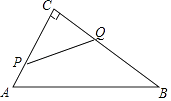A、19cm2 B、16cm2 C、15cm2 D、12cm29. 已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：x
﹣1
0
1
3
y
﹣3
1
3
1
下列结论：①抛物线的开口向下；②其图象的对称轴为x=1；③当x＜1时，函数值y随x的增大而增大；④方程ax2+bx+c=0有一个根大于4，其中正确的结论有（ ）
A、1个 B、2个 C、3个 D、4个10. 如图，垂直于x轴的直线AB分别与抛物线C1：y=x2（x≥0）和抛物线C2：y= （x≥0）交于A，B两点，过点A作CD∥x轴分别与y轴和抛物线C2交于点C，D，过点B作EF∥x轴分别与y轴和抛物线C1交于点E，F，则 的值为（ ）
A、 B、 C、 D、11. 若一次函数y=（a+1）x+a的图象过第一、三、四象限，则二次函数y=ax2﹣ax（ ）A、有最大值 B、有最大值﹣ C、有最小值 D、有最小值﹣12. 已知抛物线y= x2+1具有如下性质：该抛物线上任意一点到定点F（0，2）的距离与到x轴的距离始终相等，如图，点M的坐标为（ ，3），P是抛物线y= x2+1上一个动点，则△PMF周长的最小值是（ ）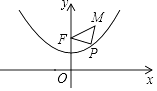
A、3 B、4 C、5 D、613. 下列关于函数 的四个命题：①当 时， 有最小值10；② 为任意实数， 时的函数值大于 时的函数值；③若 ，且 是整数，当 时， 的整数值有 个；④若函数图象过点 和 ，其中 ， ，则 ．其中真命题的序号是（ ）
A、① B、② C、③ D、④14. 已知二次函数y=x2﹣2mx（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m的值是（ ）A、 B、 C、 或 D、 或15. 二次函数y=ax2+bx+c（a、b、c是常数，且a≠0）的图象如图所示，下列结论错误的是（ ）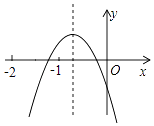
A、4ac＜b2 B、abc＜0 C、b+c＞3a D、a＜b二、填空题
-
16. 已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是 ． （只需写一个）17. 如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s的速度向点B、C、D、A匀速运动，当点E到达点B时，四个点同时停止运动，在运动过程中，当运动时间为 s时，四边形EFGH的面积最小，其最小值是 cm2 ．
18. 如图，抛物线的顶点为P（﹣2，2），与y轴交于点A（0，3）．若平移该抛物线使其顶点P沿直线移动到点P′（2，﹣2），点A的对应点为A′，则抛物线上PA段扫过的区域（阴影部分）的面积为 ．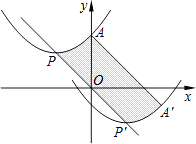
19. 如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C的坐标为（4，3），D是抛物线y=﹣x2+6x上一点，且在x轴上方，则△BCD面积的最大值为 ．
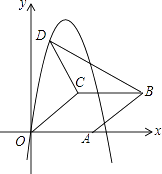20. 如图，直线y=mx+n与抛物线y=ax2+bx+c交于A（﹣1，p），B（4，q）两点，则关于x的不等式mx+n＞ax2+bx+c的解集是 ．
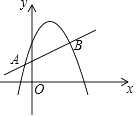21. 对于实数p，q，我们用符号min{p，q}表示p，q两数中较小的数，如min{1，2}=1，因此，min{﹣ ，﹣ }=；若min{（x﹣1）2 ， x2}=1，则x= ．
三、综合题
-
22. 已知直线y=kx+b与抛物线y=ax2（a＞0）相交于A、B两点（点A在点B的左侧），与y轴正半轴相交于点C，过点A作AD⊥x轴，垂足为D．
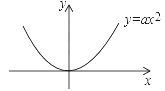(1)、若∠AOB=60°，AB∥x轴，AB=2，求a的值；(2)、若∠AOB=90°，点A的横坐标为﹣4，AC=4BC，求点B的坐标；(3)、延长AD、BO相交于点E，求证：DE=CO．23.如图，抛物线y=﹣（x﹣1）2+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．
(1)、求点B，C的坐标；(2)、判断△CDB的形状并说明理由；(3)、将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．24. 抛物线y=x2+4ax+b与x轴相交于O、A两点（其中O为坐标原点），过点P（2，2a）作直线PM⊥x轴于点M，交抛物线于点B，点B关于抛物线对称轴的对称点为C（其中B、C不重合），连接AP交y轴于点N，连接BC和PC．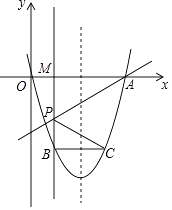
(1)、a= 时，求抛物线的解析式和BC的长；(2)、如图a＜﹣1时，若AP⊥PC，求a的值．25. 为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担．张刚按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：y=﹣10x+500．
(1)、张刚在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元？
(2)、设张刚获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？(3)、物价部门规定，这种节能灯的销售单价不得高于25元．如果张刚想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元？