备考2018年中考数学一轮基础复习:专题十三 反比例函数
试卷更新日期:2018-04-04 类型:一轮复习
一、单选题
-
1. 下列函数:①y= ;②y= ;③y=﹣ ;④y=2x﹣1中,是反比例函数的有( )A、1个 B、2个 C、3个 D、4个2. 用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I2R,下面说法正确的是( )A、P为定值,I与R成反比例 B、P为定值,I2与R成反比例 C、P为定值,I与R成正比例 D、P为定值,I2与R成正比例3. 若点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y2<y1 D、y2<y1<y34. 一次函数y1=k1x+b和反比例函数y2= (k1•k2≠0)的图象如图所示,若y1>y2 , 则x的取值范围是( )
 A、﹣2<x<0或x>1 B、﹣2<x<1 C、x<﹣2或x>1 D、x<﹣2或0<x<15. 已知直线y=kx(k>0)与双曲线y= 交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )A、﹣6 B、﹣9 C、0 D、96. 如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )
A、﹣2<x<0或x>1 B、﹣2<x<1 C、x<﹣2或x>1 D、x<﹣2或0<x<15. 已知直线y=kx(k>0)与双曲线y= 交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )A、﹣6 B、﹣9 C、0 D、96. 如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )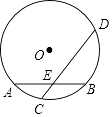 A、
A、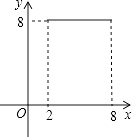 B、
B、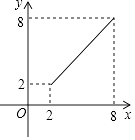 C、
C、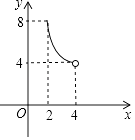 D、
D、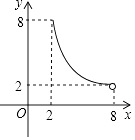 7. 如图,矩形OABC中,A(1,0),C(0,2),双曲线y= (0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF , 则k值为( )
7. 如图,矩形OABC中,A(1,0),C(0,2),双曲线y= (0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF , 则k值为( ) A、 B、1 C、 D、8. 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y= (k>0,x>0)的图象经过点C,则k的值为( )
A、 B、1 C、 D、8. 如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y= (k>0,x>0)的图象经过点C,则k的值为( )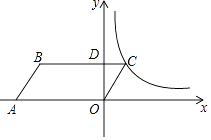 A、 B、 C、 D、9.
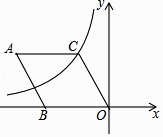
A、 B、 C、 D、9.如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y= 的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
 A、y=﹣ B、y=﹣ C、y=﹣ D、y=10. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、
A、y=﹣ B、y=﹣ C、y=﹣ D、y=10. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、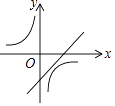 B、
B、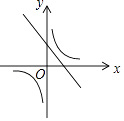 C、
C、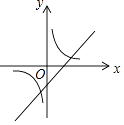 D、
D、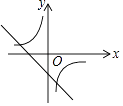 11. 已知点A在函数y1=﹣ (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )A、有1对或2对 B、只有1对 C、只有2对 D、有2对或3对12. 如图,A,B两点在反比例函数y= 的图象上,C,D两点在反比例函数y= 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( )
11. 已知点A在函数y1=﹣ (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )A、有1对或2对 B、只有1对 C、只有2对 D、有2对或3对12. 如图,A,B两点在反比例函数y= 的图象上,C,D两点在反比例函数y= 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( )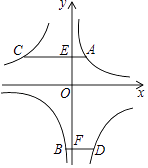 A、6 B、4 C、3 D、213. 如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y= 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
A、6 B、4 C、3 D、213. 如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y= 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )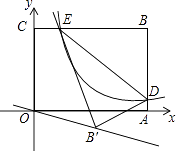 A、 B、 C、 D、14. 一次函数y=﹣x+1(0≤x≤10)与反比例函数y= (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
A、 B、 C、 D、14. 一次函数y=﹣x+1(0≤x≤10)与反比例函数y= (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )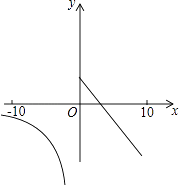 A、﹣ ≤x≤1 B、﹣ ≤x≤ C、﹣ ≤x≤ D、1≤x≤15.
A、﹣ ≤x≤1 B、﹣ ≤x≤ C、﹣ ≤x≤ D、1≤x≤15.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
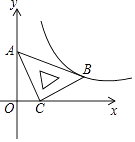 A、( ,0) B、(2,0) C、( ,0) D、(3,0)
A、( ,0) B、(2,0) C、( ,0) D、(3,0)二、填空题
-
16. 反比例函数y= 的图象经过点(1,6)和(m+1,﹣3),则m= .
17. 如果反比例函数y= (k是常数,k≠0)的图象经过点(2,3),那么在这个函数图象所在的每个象限内,y的值随x的值增大而 . (填“增大”或“减小”)18. 已知点A(a,b)在双曲线y= 上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为 .19. 如图,▱ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y= 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 20.
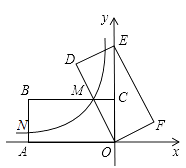
20.如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y= (x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE= ,则BN的长为 .
 21.
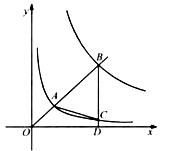
21.如图,在平面直角坐标系 中,已知直线 ( )分别交反比例函数 和 在第一象限的图象于点 , ,过点 作 轴于点 ,交 的图象于点 ,连结 .若 是等腰三角形,则 的值是 .
三、综合题
-
22. 为适应日益激烈的市场竞争要求,某工厂从2016年1月且开始限产,并对生产线进行为期5个月的升降改造,改造期间的月利润与时间成反比例;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2016年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题:
 (1)、分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;(2)、到第几个月时,该工厂月利润才能再次达到100万元?(3)、当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月?23. 如图1,一次函数y=﹣x+b与反比例函数y= (k≠0)的图象交于点A(1,3),B(m,1),与x轴交于点D,直线OA与反比例函数y= (k≠0)的图象的另一支交于点C,过点B作直线l垂直于x轴,点E是点D关于直线l的对称点.
(1)、分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;(2)、到第几个月时,该工厂月利润才能再次达到100万元?(3)、当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月?23. 如图1,一次函数y=﹣x+b与反比例函数y= (k≠0)的图象交于点A(1,3),B(m,1),与x轴交于点D,直线OA与反比例函数y= (k≠0)的图象的另一支交于点C,过点B作直线l垂直于x轴,点E是点D关于直线l的对称点.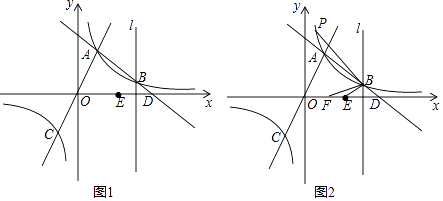 (1)、k=;(2)、判断点B,E,C是否在同一条直线上,并说明理由;(3)、如图2,已知点F在x轴正半轴上,OF= ,点P是反比例函数y= (k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).24.
(1)、k=;(2)、判断点B,E,C是否在同一条直线上,并说明理由;(3)、如图2,已知点F在x轴正半轴上,OF= ,点P是反比例函数y= (k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).24.定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
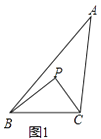
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P是△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线y= (x>0)上的任意一点,点N是x轴正半轴上的任意一点.
 (1)、
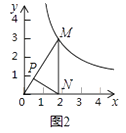
(1)、如图2,点P是OM上一点,∠ONP=∠M,试说明点P是△MON的自相似点;当点M的坐标是( ,3),点N的坐标是( ,0)时,求点P的坐标;
 (2)、
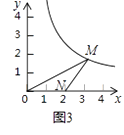
(2)、如图3,当点M的坐标是(3, ),点N的坐标是(2,0)时,求△MON的自相似点的坐标;
 (3)、是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.25.
(3)、是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.25.有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y= x与y= (k≠0)的图象性质.
小明根据学习函数的经验,对函数y= x与y= ,当k>0时的图象性质进行了探究.
下面是小明的探究过程:
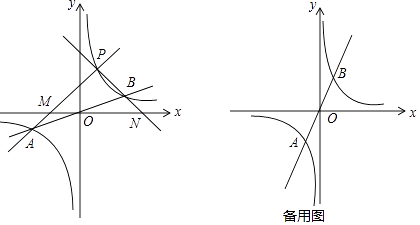 (1)、如图所示,设函数y= x与y= 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;(2)、若点P为第一象限内双曲线上不同于点B的任意一点.
(1)、如图所示,设函数y= x与y= 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;(2)、若点P为第一象限内双曲线上不同于点B的任意一点.①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下,设P(m, ),直线PA的解析式为y=ax+b(a≠0).
则 ,
解得
∴直线PA的解析式为
请你把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断△PAB的形状,并用k表示出△PAB的面积.