备考2018年中考数学一轮基础复习:专题十二 一次函数及其应用
试卷更新日期:2018-04-04 类型:一轮复习
一、单选题
-
1. 下列函数中,是一次函数的有( )
①y=πx ②y=2x﹣1 ③y= ④y=2﹣3x ⑤y=x2﹣1.
A、4个 B、3个 C、2个 D、1个2. 公式L=L0+KP表示当重力为P时的物体作用在弹簧上时弹簧的长度,L0代表弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧拉伸的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( )A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P3. 如图,在同一平面直角坐标系中,反比例函数y= 与一次函数y=kx-1(k为常数,且k>0)的图象可能是( )A、 B、
B、 C、
C、 D、
D、 4. 二次函数y=a(x+m)2+n的图象如图所示,则一次函数y=mx+n的图象经过( )
4. 二次函数y=a(x+m)2+n的图象如图所示,则一次函数y=mx+n的图象经过( ) A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限5. 若一次函数y=kx+b,当x的值减小1,y的值就减小2,则当x的值增加2时,y的值( )
A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限5. 若一次函数y=kx+b,当x的值减小1,y的值就减小2,则当x的值增加2时,y的值( )
A、增加4 B、减小4 C、增加2 D、减小26. 直线l:y=mx﹣m+1(m为常数,且m≠0)与坐标轴交于A、B两点,若△AOB(O是原点)的面积恰为2,则符合要求的直线l有( )A、1条 B、2条 C、3条 D、4条7. 如图,等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t.则大致反映S与t变化关系的图象是( )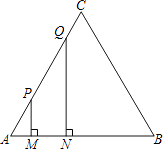 A、
A、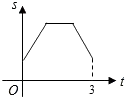 B、
B、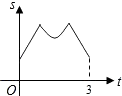 C、
C、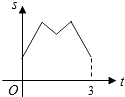 D、
D、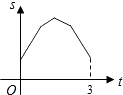 8. 小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
8. 小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A、1个 B、2个 C、3个 D、4个9. 若直线y=﹣x+a与直线y=x+b的交点坐标为(2,8),则a﹣b的值为( )
A、2 B、4 C、6 D、810. 已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )A、0<y1<y2 B、y1<0<y2 C、y1<y2<0 D、y2<0<y111. 已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )A、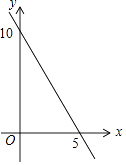 B、
B、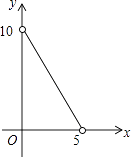 C、
C、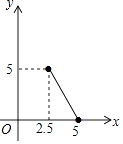 D、
D、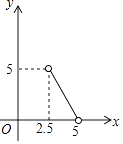 12. 若直线y=kx+k+1经过点(m,n+3)和(m+1,2n﹣1),且0<k<2,则n的值可以是( )A、3 B、4 C、5 D、613. 已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )A、k<2,m>0 B、k<2,m<0 C、k>2,m>0 D、k<0,m<014.
12. 若直线y=kx+k+1经过点(m,n+3)和(m+1,2n﹣1),且0<k<2,则n的值可以是( )A、3 B、4 C、5 D、613. 已知一次函数y=kx﹣m﹣2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )A、k<2,m>0 B、k<2,m<0 C、k>2,m>0 D、k<0,m<014.将2×2的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )
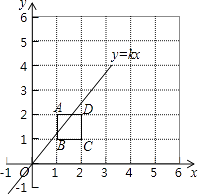 A、3 B、2 C、1 D、15.
A、3 B、2 C、1 D、15.如图,直线y= x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
 A、(﹣3,0) B、(﹣6,0) C、(﹣ ,0) D、(﹣ ,0)
A、(﹣3,0) B、(﹣6,0) C、(﹣ ,0) D、(﹣ ,0)二、填空题
-
16. 已知点P(1,2)关于x轴的对称点为P′,且P′在直线y=kx+3上,把直线y=kx+3的图象向上平移2个单位,所得的直线解析式为 .17. 我们规定:当k,b为常数,k≠0,b≠0,k≠b时,一次函数y=kx+b与y=bx+k互为交换函数.例如:y=4x+3的交换函数为y=3x+4.一次函数y=kx+2与它的交换函数图象的交点横坐标为 .18. 如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为 .
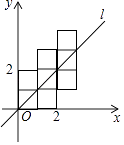 19. 如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx﹣6<ax+4<kx的解集为 .
19. 如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx﹣6<ax+4<kx的解集为 .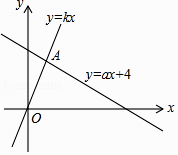 20. A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是米.
20. A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是米. 21. 如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y= x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y= x于点B3 , …,按照此规律进行下去,则点An的横坐标为 .
21. 如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y= x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y= x于点B3 , …,按照此规律进行下去,则点An的横坐标为 .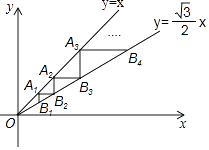
三、综合题
-
22. 如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
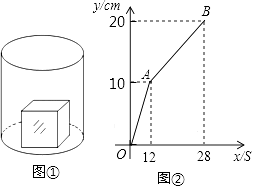 (1)、正方体的棱长为cm;(2)、求线段AB对应的函数解析式,并写出自变量x的取值范围;(3)、如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.23.
(1)、正方体的棱长为cm;(2)、求线段AB对应的函数解析式,并写出自变量x的取值范围;(3)、如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.23.小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2= 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= ,y= .
 (1)、请你帮小明写出中点坐标公式的证明过程;(2)、①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;
(1)、请你帮小明写出中点坐标公式的证明过程;(2)、①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;
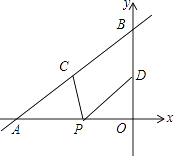
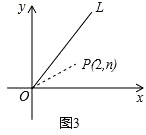
(3)、如图3,点P(2,n)在函数y= x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
 24. 阅读材料:
24. 阅读材料:在平面直角坐标系xOy中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为:d= .
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴点P0(0,0)到直线4x+3y﹣3=0的距离为d= = .
根据以上材料,解决下列问题:
(1)、点P1(3,4)到直线y=﹣ x+ 的距离为;(2)、已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣ x+b相切,求实数b的值;(3)、如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值.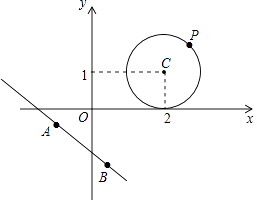 25.
25.“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
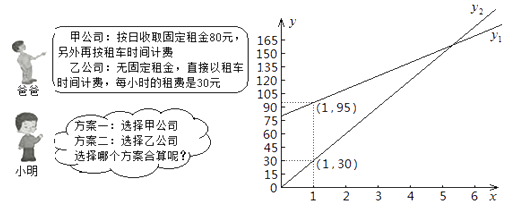
根据以上信息,解答下列问题:
(1)、设租车时间为 小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为 元,分别求出 , 关于 的函数表达式;(2)、请你帮助小明计算并选择哪个出游方案合算。