河南省2017-2018学年高三上学期理数高三一轮复习诊断调研联考联考试卷
试卷更新日期:2018-04-04 类型:高考模拟
一、单选题
-
1. 已知 ,复数 ,若 ,则 ( )A、 B、 C、 D、2. 已知集合 , ,则 ( )A、 B、 C、 D、3. 某城市收集并整理了该市2017年1月份至10月份各月最低气温与最高气温(单位: )的数据,绘制了下面的折线图。
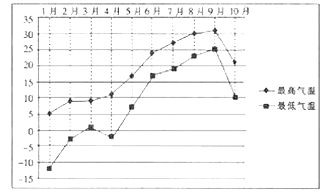
已知该市的各月最低气温与最高气温具有较好的线性关系,则根据该折线图,下列结论错误的是( )
A、最低气温与最高气温为正相关 B、10月的最高气温不低于5月的最高气温 C、月温差(最高气温减最低气温)的最大值出现在1月 D、最低气温低于 的月份有4个4. 在等比数列 中,若 , ,则 ( )A、 B、 C、 D、5. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有阳马,广五尺,袤七尺,高八尺,问积几何?”其意思为:“今有底面为矩形,一侧棱垂直于底面的四棱锥,它的底面长、宽分别为7尺和5尺,高为8尺,问它的体积是多少?”若以上的条件不变,则这个四棱锥的外接球的表面积为( )A、 平方尺 B、 平方尺 C、 平方尺 D、 平方尺6. 定义 表示不超过 的最大整数, ,例如 , ,执行如图所示的程序框图,若输入的 ,则输出的 ( ) A、 B、 C、 D、7. 若对于任意 都有 ,则函数 图象的对称中心为( )A、 ( ) B、 ( ) C、 ( ) D、 ( )8. 设 , 满足约束条件 若 取得最大值的最优解不唯一,则实数 的值为( )A、 或 B、 或 C、 或 D、 或29. 函数 的部分图象大致是( )A、
A、 B、 C、 D、7. 若对于任意 都有 ,则函数 图象的对称中心为( )A、 ( ) B、 ( ) C、 ( ) D、 ( )8. 设 , 满足约束条件 若 取得最大值的最优解不唯一,则实数 的值为( )A、 或 B、 或 C、 或 D、 或29. 函数 的部分图象大致是( )A、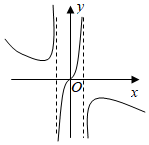 B、
B、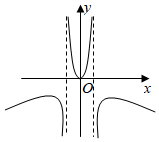 C、
C、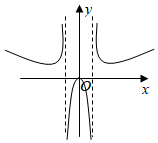 D、
D、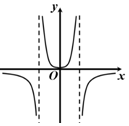 10. 已知某几何体的三视图如图所示,则该几何体的表面积为( )
10. 已知某几何体的三视图如图所示,则该几何体的表面积为( ) A、 B、 C、 D、11. 设椭圆 : 的一个焦点为 ,点 为椭圆 内一点,若椭圆 上存在一点 ,使得 ,则椭圆 的离心率的取值范围是( )A、 B、 C、 D、12. 已知函数 ,其中 是自然对数的底数,若不等式 恒成立,则 的最小值为( )A、 B、 C、 D、
A、 B、 C、 D、11. 设椭圆 : 的一个焦点为 ,点 为椭圆 内一点,若椭圆 上存在一点 ,使得 ,则椭圆 的离心率的取值范围是( )A、 B、 C、 D、12. 已知函数 ,其中 是自然对数的底数,若不等式 恒成立,则 的最小值为( )A、 B、 C、 D、二、填空题
-
13. 在 中, , ,则 .
14. 已知 , ,若 ,则 .15. 已知 为数列 的前 项和, ,当 时,恒有 成立,若 ,则 .16. 设 , 分别是双曲线 ( , )的左、右焦点,过 的直线 与双曲线分别交于 , ,且 在第一象限,若 为等边三角形,则双曲线的实轴长为 .
三、解答题
-
17. 如图,在 中,内角 , , 的对边分别为 , , ,已知 , , , , 分别为线段 上的点,且 , .
 (1)、求线段 的长;(2)、求 的面积.18. 某班为了活跃元旦晚会气氛,主持人请12位同学做一个游戏,第一轮游戏中,主持人将标有数字1到12的十二张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字7到12的卡片的同学留下,其余的淘汰;第二轮将标有数字1到6的六张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字4到6的卡片的同学留下,其余的淘汰;第三轮将标有数字1,2,3的三张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字2,3的卡片的同学留下,其余的淘汰;第四轮用同样的办法淘汰一位同学,最后留下的这位同学获得一个奖品.已知同学甲参加了该游戏.(1)、求甲获得奖品的概率;(2)、设 为甲参加游戏的轮数,求 的分布列与数学期望.19. 如图,在三棱台 中, , 分别是 , 的中点, 平面 , 是等边三角形, , , .
(1)、求线段 的长;(2)、求 的面积.18. 某班为了活跃元旦晚会气氛,主持人请12位同学做一个游戏,第一轮游戏中,主持人将标有数字1到12的十二张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字7到12的卡片的同学留下,其余的淘汰;第二轮将标有数字1到6的六张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字4到6的卡片的同学留下,其余的淘汰;第三轮将标有数字1,2,3的三张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字2,3的卡片的同学留下,其余的淘汰;第四轮用同样的办法淘汰一位同学,最后留下的这位同学获得一个奖品.已知同学甲参加了该游戏.(1)、求甲获得奖品的概率;(2)、设 为甲参加游戏的轮数,求 的分布列与数学期望.19. 如图,在三棱台 中, , 分别是 , 的中点, 平面 , 是等边三角形, , , .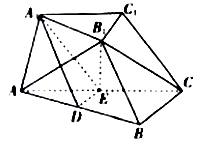 (1)、证明: 平面 ;(2)、求二面角 的正弦值.20. 已知抛物线 : ,斜率为 且过点 的直线 与 交于 , 两点,且 ,其中 为坐标原点.(1)、求抛物线 的方程;(2)、设点 ,记直线 , 的斜率分别为 , ,证明: 为定值.21. 已知函数 ( ),且 是它的极值点.(1)、求 的值;(2)、求 在 上的最大值;(3)、设 ,证明:对任意 , 都有 .
(1)、证明: 平面 ;(2)、求二面角 的正弦值.20. 已知抛物线 : ,斜率为 且过点 的直线 与 交于 , 两点,且 ,其中 为坐标原点.(1)、求抛物线 的方程;(2)、设点 ,记直线 , 的斜率分别为 , ,证明: 为定值.21. 已知函数 ( ),且 是它的极值点.(1)、求 的值;(2)、求 在 上的最大值;(3)、设 ,证明:对任意 , 都有 .