2015-2016学年广东省汕头市潮南区七年级下学期期末数学试卷
试卷更新日期:2016-11-28 类型:期末考试
一、选择题
-
1. 在平面直角坐标系中,点P(2,﹣3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 为了描述温州市某一天气温变化情况,应选择( )A、扇形统计图 B、折线统计图 C、条形统计图 D、直方图3. 利用数轴确定不等式组的解集,正确的是( )
A、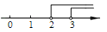 B、
B、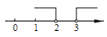 C、
C、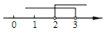 D、
D、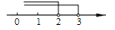 4. 若a>b,则下列不等式变形错误的是( )A、a+1>b+1 B、 C、3a﹣4>3b﹣4 D、4﹣3a>4﹣3b5. 已知正方形的面积是17,则它的边长在( )A、5与6之间 B、4与5之间 C、3与4之间 D、2与3之间6. 将一直角三角板与两边平行的纸条如图放置.已知∠1=30°,则∠2的度数为( )
4. 若a>b,则下列不等式变形错误的是( )A、a+1>b+1 B、 C、3a﹣4>3b﹣4 D、4﹣3a>4﹣3b5. 已知正方形的面积是17,则它的边长在( )A、5与6之间 B、4与5之间 C、3与4之间 D、2与3之间6. 将一直角三角板与两边平行的纸条如图放置.已知∠1=30°,则∠2的度数为( )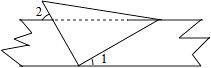 A、30° B、45° C、50° D、60°7. 点A(﹣3,﹣2)向上平移2个单位,再向右平移2个单位到点B,则点B的坐标为( )A、(1,0) B、(1,﹣4) C、(﹣1,0) D、(﹣5,﹣1)8.
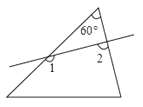
A、30° B、45° C、50° D、60°7. 点A(﹣3,﹣2)向上平移2个单位,再向右平移2个单位到点B,则点B的坐标为( )A、(1,0) B、(1,﹣4) C、(﹣1,0) D、(﹣5,﹣1)8.如图,一个60°的角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
 A、120° B、180° C、240° D、300°9. 以下五个条件中,能得到互相垂直关系的有( )
A、120° B、180° C、240° D、300°9. 以下五个条件中,能得到互相垂直关系的有( )①对顶角的平分线;
②邻补角的平分线;
③平行线截得的一组同位角的平分线;
④平行线截得的一组内错角的平分线;
⑤平行线截得的一组同旁内角的平分线.
A、1个 B、2个 C、3个 D、4个10. 如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )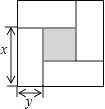 A、x+y=7 B、x﹣y=2 C、x2﹣y2=4 D、4xy+4=49
A、x+y=7 B、x﹣y=2 C、x2﹣y2=4 D、4xy+4=49二、填空题
-
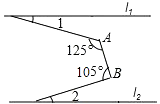
11. 化简: = .12. 不等式2x+5>4x﹣1的正整数解是13. 已知,若B(﹣2,0),A为象限内一点,且点A坐标是二元一次方程x+y=0的一组解,请你写出一个满足条件的点A坐标(写出一个即可),此时△ABO的面积为 .14. 如图,直线l1∥l2 , ∠A=125°,∠B=105°,则∠1+∠2=°.
 15. 如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 .
15. 如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 .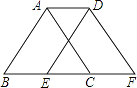 16.
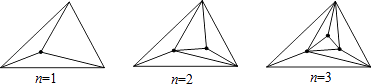
16.一个三角形内有n个点,在这些点及三角形顶点之间用线段连接起来,使得这些线段互不相交,且又能把原三角形分割为不重叠的小三角形.如图:若三角形内有1个点时此时有3个小三角形;若三角形内有2个点时,此时有5个小三角形.则当三角形内有3个点时,此时有个小三角形;当三角形内有n个点时,此时有个小三角形.
三、解答题(一)
-
17. 计算: +4× + ( ﹣1).18. 解方程组: .19. 求不等式组 的整数解.
四、解答题(二)
-
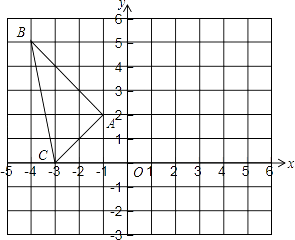
20. 如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,请画出平移后的图形,并写出△A′B′C′各顶点的坐标.
 21. 铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为多少厘米?22. 某文具店有单价为10元、15元和20元的三种文具盒出售,该商店统计了2014年3月份这三种文具盒的销售情况,并绘制统计图(不完整)如下:
21. 铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为多少厘米?22. 某文具店有单价为10元、15元和20元的三种文具盒出售,该商店统计了2014年3月份这三种文具盒的销售情况,并绘制统计图(不完整)如下: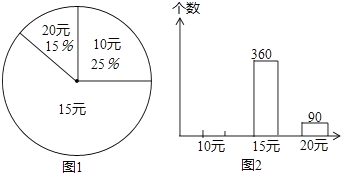 (1)、这次调查中一共抽取了多少个文具盒?(2)、求出图1中表示“15元”的扇形所占圆心角的度数;(3)、在图2中把条形统计图补充完整.
(1)、这次调查中一共抽取了多少个文具盒?(2)、求出图1中表示“15元”的扇形所占圆心角的度数;(3)、在图2中把条形统计图补充完整.五、解答题(三)
-
23. 如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于F.
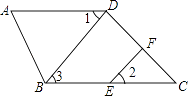 (1)、求证:AD∥BC;(2)、若∠1=36°,求∠2的度数.24. 某公式为了扩大生产,决定购进6台机器,但所用资金不能超过68万元,现有甲、乙两种机器供选择,其中甲种机器每台14万元,乙种机器每台10万元,现按该公司要求有哪几种购买方案,并说明理由.25. 在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;(1)、如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;
(1)、求证:AD∥BC;(2)、若∠1=36°,求∠2的度数.24. 某公式为了扩大生产,决定购进6台机器,但所用资金不能超过68万元,现有甲、乙两种机器供选择,其中甲种机器每台14万元,乙种机器每台10万元,现按该公司要求有哪几种购买方案,并说明理由.25. 在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;(1)、如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;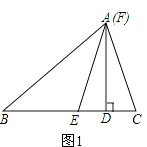 (2)、如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.
(2)、如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.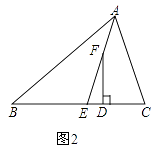 (3)、如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.
(3)、如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.