江苏省扬州市江都区五校2018届九年级下学期数学第一次月考试卷
试卷更新日期:2018-04-03 类型:月考试卷
一、选择题
-
1. 下列各数中,-3的倒数是( )A、3 B、 C、 D、-32. 在下面四个几何体中,俯视图是三角形的是( )
A、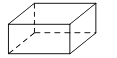 B、
B、 C、
C、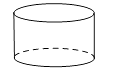 D、
D、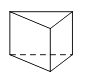 3. 下列运算正确的是( )A、a·a2=a2 B、 C、 D、4. 使分式 有意义的x的取值范围是( )
3. 下列运算正确的是( )A、a·a2=a2 B、 C、 D、4. 使分式 有意义的x的取值范围是( )
A、 x≥2 B、x>2 C、x<2 D、x≠25. 用直尺和圆规作一个角等于已知角,如图,能得出 的依据是( )
A、(SAS) B、(SSS) C、(AAS) D、(A SA)6. 下列说法正确的是( )A、一个游戏中奖的概率是 ,则做100次这样的游戏一定会中奖 B、为了了解全国中学生的心理健康状况,应采用普查的方式 C、一组数据0,1,2,1,1的众数和中位数都是1 D、若甲组数据的方差S甲2=0.2,乙组数据的方差S乙2=0.5,则乙组数据比甲组数据稳定7. 已知点(x1 , y1)、(x2 , y2)、(x3 , y3)在双曲线y= 上,当x1<0<x2<x3时,y1、y2、y3的大小关系是( )
A、y1<y2<y3 B、y1<y3<y2 C、y3<y1<y2 D、y2<y3<y18. 如图,在△ABC中, AB=3,AC=2.当∠B最大时,BC的长是( )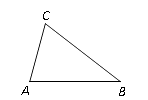 A、1 B、5 C、 D、
A、1 B、5 C、 D、二、填空题
-
9. 16的平方根是 .10. 已知一粒大米的质量约为0.000021千克,该重量用科学记数法表示为千克11. 分解因式:x3y﹣4xy= .12. 一个正八边形每个内角的度数为度13. 如果关于x的一元二次方程mx2﹣6x+1=0有两个不相等的实数根,则m的取值范围是 .
14. 如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的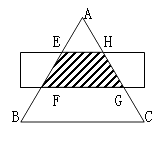 15. 如图,在⊙o中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=度.
15. 如图,在⊙o中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=度.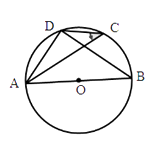 16. 用一个半径为 30cm,面积为 300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为cm
16. 用一个半径为 30cm,面积为 300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为cm
17. 已知二次函数y=ax2+bx+c的部分图像如图所示,则关于x的方程ax2+bx+c=0的两个根的和等于 .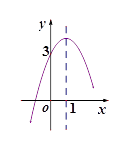 18. 在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .
18. 在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .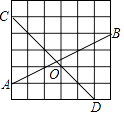
三、解答题
-
19. 计算题
(1)、计算:(-4)0+()-1-2cos30°-;(2)、解不等式组:20. 先化简,再求值:( x+1- )÷ ,其中x=2.21. 设中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.请根据图中的信息,解答下列问题: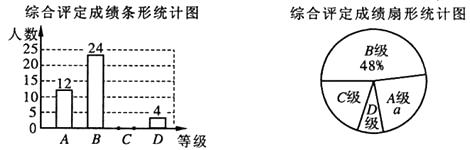 (1)、在这次调查中,一共抽取了名学生,A级所占的百分比a=;
(1)、在这次调查中,一共抽取了名学生,A级所占的百分比a=;
(2)、补全条形统计图;
(3)、扇形统计图中C级对应的圆心角为多少度;
(4)、若该校共有2000名学生,请你估计该校D级学生有多少名?
22. 某网上书城“五一·劳动节”期间在特定的书目中举办特价促销活动,有A、B、C、D四本书是小明比较中意的,但是他只打算选购两本,求下列事件的概率:(1)、小明购买A书,再从其余三本书中随机选一款,恰好选中C的概率是(2)、小明随机选取两本书,请用树状图或列表法求出他恰好选中A、C两本的概率.23. 为了响应学校提出的“节能减排,低碳生活”的倡议,班会课上小明建议每位同学都践行“双面打印,节约用纸”.他举了一个实际例子:打印一份资料,如果用A4厚型纸单面打印,总质量为400克,若将其全部改成双面打印,用纸将减少一半;现用A4薄型纸双面打印,总质量仅为160克.已知每页薄型纸比厚型纸轻0.8克,求例子中的A4厚型纸每页的质量.(墨的质量忽略不计)提示:总质量=每页纸的质量×纸张数
24. 如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.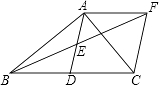 (1)、求证:AD=AF;
(1)、求证:AD=AF;
(2)、如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.25. 如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.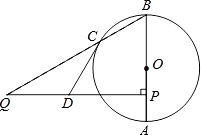 (1)、点D在线段PQ上,且DQ=DC.求证:CD是⊙O的切线;(2)、若sin∠Q= ,BP=6,AP=2,求QC的长.
(1)、点D在线段PQ上,且DQ=DC.求证:CD是⊙O的切线;(2)、若sin∠Q= ,BP=6,AP=2,求QC的长.
26. 我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)= .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= .(1)、若F(a)= 且a为100以内的正整数,则a=
(2)、如果m是一个两位数,那么试问F(m)是否存在最大值或最小值?若存在,求出最大(或最小)值以及此时m的取值并简要说明理由。27. 如图1,在平面直角坐标系中,O为坐标原点,点A(-1,0),点B(0, ).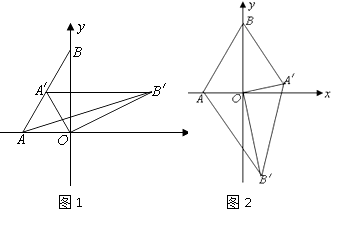 (1)、求∠BAO的度数;
(1)、求∠BAO的度数;
(2)、如图1,将△AOB绕点O顺时针旋转得△A′OB′,当点A′恰好落在AB边上时,设△A′BO的面积为S1。 , △AB′O的面积为S2 , S1与S2有何关系?为什么?
(3)、若将△AOB绕点O顺时针旋转到如图2所示的位置时,S1与S2的关系发生变化了吗?证明你的判断.
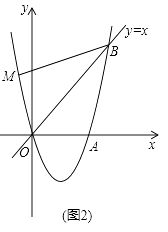
28. 如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A( ,0),在第一象限内与直线y=x交于点B(2,t).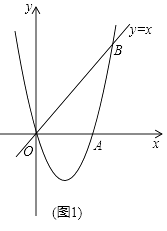 (1)、求这条抛物线的表达式;(2)、在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)、如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求这条抛物线的表达式;(2)、在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)、如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.