江苏省扬州市江都区五校2017-2018学年八年级下学期数学第一次月考试卷
试卷更新日期:2018-04-03 类型:月考试卷
一、选择题
-
1. 下列汽车标志中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列调查中,适合用全面调查方法的是 ( )A、了解一批电视机的使用寿命 B、了解我市居民的年人均收入 C、了解我市中学生的近视率 D、了解某校数学教师的年龄状况3. 如图的两个统计图,女生人数多的学校是( )
2. 下列调查中,适合用全面调查方法的是 ( )A、了解一批电视机的使用寿命 B、了解我市居民的年人均收入 C、了解我市中学生的近视率 D、了解某校数学教师的年龄状况3. 如图的两个统计图,女生人数多的学校是( ) A、甲校 B、乙校 C、甲、乙两校一样多 D、无法确定4. 矩形具有而菱形不具有的性质是( )A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、两组对角分别相等5. 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
A、甲校 B、乙校 C、甲、乙两校一样多 D、无法确定4. 矩形具有而菱形不具有的性质是( )A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、两组对角分别相等5. 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )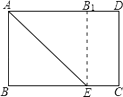 A、3cm B、2cm C、1cm D、0.5cm6. 如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG﹥60⁰,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )
A、3cm B、2cm C、1cm D、0.5cm6. 如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG﹥60⁰,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )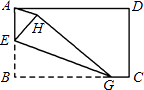
A、4个 B、3个 C、2个 D、1个7. 如图,正方形 的面积为9 . 是等边三角形,点 在正方形 内,在对 角线 上有一点 ,使 的和最小,则这个最小值为( ).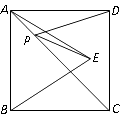 A、3 B、 C、 D、8. 在正方形ABCD中,点E为BC边的中点,点
A、3 B、 C、 D、8. 在正方形ABCD中,点E为BC边的中点,点 与点B关于AE对称,
与点B关于AE对称, 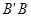 与AE交于点F,连接
与AE交于点F,连接 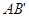 ,
, 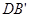 ,FC。下列结论:①
,FC。下列结论:① 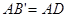 ;②
;② 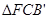 为等腰直角三角形;③
为等腰直角三角形;③ 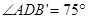 ;④
;④ 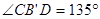 。其中正确的是( )
。其中正确的是( )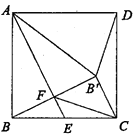 A、①② B、①②④ C、③④ D、①②③④
A、①② B、①②④ C、③④ D、①②③④二、填空题
-
9. 某班在大课间活动中抽查了20名学生每分钟跳绳次数,得到如下数据(单位:次):50,63,77,83,87,88,89,9l,93,100,102,111,117,121,130,133,146,158,177,188.则跳绳次数在90~110这一组的频率是.
10. 一个不透明的口袋里装有若干除颜色外其他完全相同的小球,其中有6个黄球,将口袋中的球摇匀,从中任意摸出一个球记下颜色后再放回,通过大量重复上述实验后发现,摸到黄球的频率稳定在30%,由此估计口袋中共有小球个.
11. 如图,在平行四边形ABCD中,对角线交于点0,点E、F在直线AC上(不同于A、C),当E、F的位置满足的条件时,四边形DEBF是平行四边形.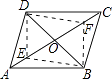 12. 如图,把Rt△ABC绕点A逆时针旋转46°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=。
12. 如图,把Rt△ABC绕点A逆时针旋转46°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=。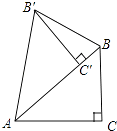 13. 矩形的两条对角线的夹角为60⁰,一条对角线与较短边的和为18,则较长边的长为 .14. 如图,在周长为22的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE BD,交AD于点E,则△CDE的周长为
13. 矩形的两条对角线的夹角为60⁰,一条对角线与较短边的和为18,则较长边的长为 .14. 如图,在周长为22的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE BD,交AD于点E,则△CDE的周长为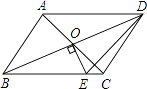 15. 如图,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于点E,交BC于点F,∠BDF=15°,则∠COF=°.
15. 如图,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于点E,交BC于点F,∠BDF=15°,则∠COF=°.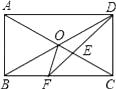 16. 如图,菱形ABCD的面积为12cm2 , 正方形AECF的面积为8cm2 , 则菱形的边长为 cm.
16. 如图,菱形ABCD的面积为12cm2 , 正方形AECF的面积为8cm2 , 则菱形的边长为 cm.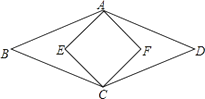 17. 在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过秒该直线可将平行四边形OABC的面积平分.
17. 在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过秒该直线可将平行四边形OABC的面积平分.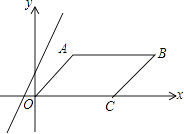 18. 小明尝试着将矩形纸片 (如图(1) , )沿过点 的直线折叠,使得点 落在边 上的点 处,折痕为 (如图(2));再沿过点 的直线折叠,使得点 落在边 上的点 处,点 落在边 上的点 处,折痕为 (如图(3)).如果第二次折叠后,点 正好在 的平分线上,那么矩形 长与宽的比值为 .
18. 小明尝试着将矩形纸片 (如图(1) , )沿过点 的直线折叠,使得点 落在边 上的点 处,折痕为 (如图(2));再沿过点 的直线折叠,使得点 落在边 上的点 处,点 落在边 上的点 处,折痕为 (如图(3)).如果第二次折叠后,点 正好在 的平分线上,那么矩形 长与宽的比值为 .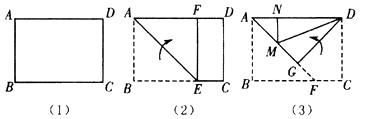
三、解答题
-
19. 在平面直角坐标系 中的位置如图所示.
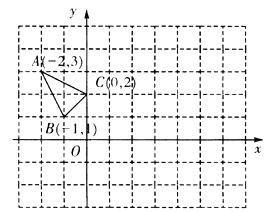 (1)、作 关于点 成中心对称的 .(2)、将 向右平移4个单位,作出平移后的 .(3)、在 轴上求作一点 ,使 的值最小
(1)、作 关于点 成中心对称的 .(2)、将 向右平移4个单位,作出平移后的 .(3)、在 轴上求作一点 ,使 的值最小
20. 下表记录了一名球员在罚球线上投篮的结果,投篮次数(n)
50
100
150
209
250
300
350
投中次数(m)
28
60
78
104
123
152
175
投中频率(n/m)
0.56
0.60
0.49
(1)、计算并填写表中的投中频率(精确到0.01);(2)、这名球员投篮一次,投中的概率约是多少(精确到0.1)?
21. 某校在“6·26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题: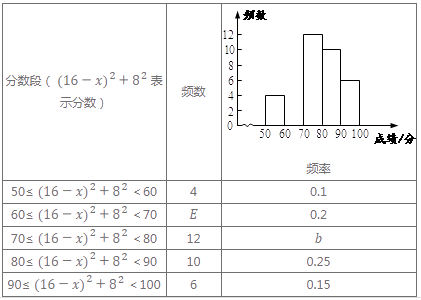
(1)、表中 = , = , 并补全直方图;(2)、若用扇形统计图描述此成绩统计分布情况,则分数段80≤ <100对应扇形的圆心角度数是;(3)、请估计该年级分数在60≤ <70的学生有多少人?22. 如图,BC是等腰三角形BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.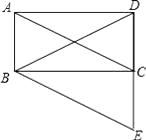 23. 如图,在四边形ABCD中,AB=BC , 对角线BD平分∠ABC , P是BD上一点,过点P作PM⊥AD , PN⊥CD , 垂足分别为M、N.
23. 如图,在四边形ABCD中,AB=BC , 对角线BD平分∠ABC , P是BD上一点,过点P作PM⊥AD , PN⊥CD , 垂足分别为M、N.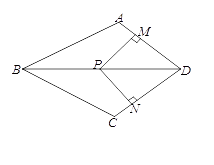 (1)、求证:∠ADB=∠CDB;
(1)、求证:∠ADB=∠CDB;
(2)、若∠ADC=90°,求证:四边形MPND是正方形.24. 如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证: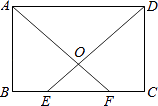 (1)、△ABF≌△DCE;(2)、△AOD是等腰三角形.25. 如图,在四边形ABCD中,AD∥BC,AD≠BC,∠B=90⁰,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
(1)、△ABF≌△DCE;(2)、△AOD是等腰三角形.25. 如图,在四边形ABCD中,AD∥BC,AD≠BC,∠B=90⁰,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.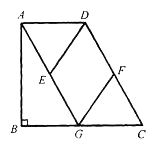 (1)、求证:四边形DEGF是平行四边形;(2)、当点G是BC的中点时,求证:四边形DEGF是菱形26. 如图,正方形ABCD中,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF、CF.
(1)、求证:四边形DEGF是平行四边形;(2)、当点G是BC的中点时,求证:四边形DEGF是菱形26. 如图,正方形ABCD中,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF、CF.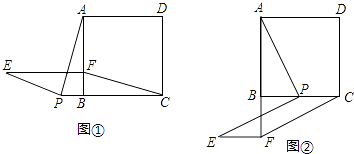 (1)、如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形.(2)、如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由.27. 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
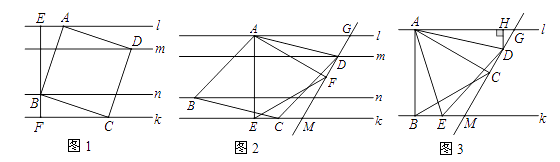
(1)、如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形.(2)、如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由.27. 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG. (1)、求证:△CBG≌△CDG;(2)、求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;(3)、连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.28. 【背景】已知: ∥m∥n∥k , 平行线 与m、m与n、n与k之间的距离分别为d1 , d2 , d3 , 且d1=d3=1,d2=2.我们把四个顶点分别在 ,m , n , k这四条平行线上的四边形称为“格线四边形” .(1)、【探究1】如图1,正方形ABCD为“格线四边形”,BE⊥ 于点E , BE的反向延长线交直线k于点F.求正方形ABCD的边长.(2)、【探究2】如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E , ∠AFD=90°,直线DF分别交直线 ,k于点G、点M.求证:EC=DF .(3)、【拓展】如图3, ∥k , 等边△ABC的顶点A , B分别落在直线 l , k上,AB⊥k于点B , 且∠ACD=90°,直线CD分别交直线 、k于点G、点M , 点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE , DH⊥ 于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.
(1)、求证:△CBG≌△CDG;(2)、求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;(3)、连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.28. 【背景】已知: ∥m∥n∥k , 平行线 与m、m与n、n与k之间的距离分别为d1 , d2 , d3 , 且d1=d3=1,d2=2.我们把四个顶点分别在 ,m , n , k这四条平行线上的四边形称为“格线四边形” .(1)、【探究1】如图1,正方形ABCD为“格线四边形”,BE⊥ 于点E , BE的反向延长线交直线k于点F.求正方形ABCD的边长.(2)、【探究2】如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E , ∠AFD=90°,直线DF分别交直线 ,k于点G、点M.求证:EC=DF .(3)、【拓展】如图3, ∥k , 等边△ABC的顶点A , B分别落在直线 l , k上,AB⊥k于点B , 且∠ACD=90°,直线CD分别交直线 、k于点G、点M , 点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE , DH⊥ 于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.