2015-2016学年广东省广州市番禺区八年级上学期期末数学试卷
试卷更新日期：2016-11-28 类型：期末考试
一、选择题
-
1. 计算（﹣a3）3的结果正确是（ ）A、﹣ B、﹣ C、﹣ D、2. 若等腰三角形的底角为40°，则它的顶角度数为（ ）A、40° B、100° C、80° D、70°3.
下列几何图形中，一定是轴对称图形的有（ ）
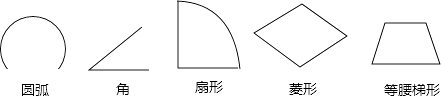A、5个 B、4个 C、3个 D、2个4. 下列运算正确的是（ ）A、x2÷x2=1 B、（﹣a2b）3=a6b3 C、（﹣3x）0=﹣1 D、（x+3）2=x2+95.如图，AB∥CD，∠D=∠E=30°，则∠B的度数为（ ）
A、50° B、60° C、70° D、80°6. 要时分式 有意义，则x应满足的条件为（ ）A、x≠2 B、x≠0 C、x≠±2 D、x≠﹣27.如图，在△ABC中，∠B=30°，ED垂直平分BC，ED=5．则CE的长为（ ）
A、20 B、12 C、10 D、88.如图，阴影部分是由5个小正方形涂黑组成的一个直角图形，再将方格内空白的两个小正方形涂黑，得到新的图形（阴影部分），其中不是轴对称图形的是（ ）
A、
B、
C、
D、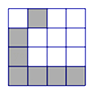
9. 已知点P（a，3）、Q（﹣2，b）关于y轴对称，则 =（ ）A、﹣5 B、5 C、﹣ D、10. 如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB=65°，则∠AED′等于（ ）
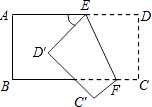A、70° B、65° C、50° D、25°二、填空题
-
11. 计算：a﹣2÷a﹣5= ．12. 化简： = ．13. 若等腰三角形两边长分别为3和5，则它的周长是 ．14. 如图，在△ABC中，分别以点A和点B为圆心，大于 AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB=7，则△ABC的周长为 ．
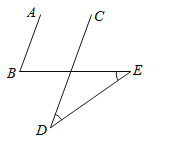
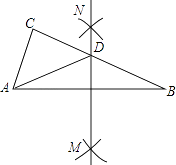15. 如图，CD与BE互相垂直平分，AD⊥DB，交BE延长线于点A，连接AC，已知∠BDE=70°，则∠CAD= ．
三、解答题
-
16. 分解因式：(1)、ax﹣ay；(2)、x2﹣y4；(3)、﹣x2+4xy﹣4y2 ．17. 如图，点A，F，C，D在同一直线上，点B和E分别在直线AD的两侧，AB∥DE且AB=DE，AF=DC．求证：
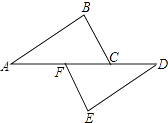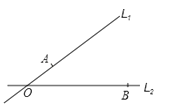
(1)、AC=DF；(2)、BC∥EF．18.如图，有分别过A、B两个加油站的公路l1、l2相交于点O，现准备在∠AOB内建一个油库，要求油库的位置点P满足到A、B两个加油站的距离相等，而且P到两条公路l1、l2的距离也相等．请用尺规作图作出点P（不写作法，保留作图痕迹）
19. 在如图所示的方格纸中．
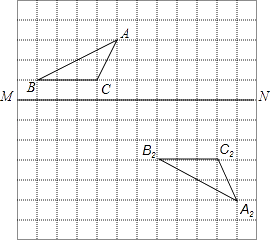(1)、作出△ABC关于MN对称的图形△A1B1C1；(2)、说明△A2B2C2是由△A1B1C1经过怎样的平移变换得到的？(3)、若点A在直角坐标系中的坐标为（﹣1，3），试写出A1、B1、C2坐标．20. 已知 = ，求 的值．21. 计算与解方程(1)、计算：（7x2y3﹣8x3y2z）÷8x2y2；(2)、解分式方程： ．22.如图，在△ABC中，AB=c，AC=b．AD是△ABC的角平分线，DE⊥A于E，DF⊥AC于F，EF与AD相交于O，已知△ADC的面积为1．
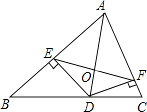(1)、证明：DE=DF；(2)、试探究线段EF和AD是否垂直？并说明理由；(3)、若△BDE的面积是△CDF的面积2倍．试求四边形AEDF的面积．23. 为了“绿色出行”，减少雾霾，家住番禺在广州中心城区上班的王经理，上班出行由自驾车改为乘坐地铁出行，已知王经理家距上班地点21千米，他用地铁方式平均每小时出行的路程，比他用自驾车平均每小时行驶的路程的2倍还多5千米，他从家出发到达上班地点，地铁出行所用时间是自驾车方式所用时间的 ．求王经理地铁出行方式上班的平均速度．24. △ABC为等腰直角三角形，∠ABC=90°，点D在AB边上（不与点A，B重合），以CD为腰作等腰直角△CDE，∠DCE=90°．
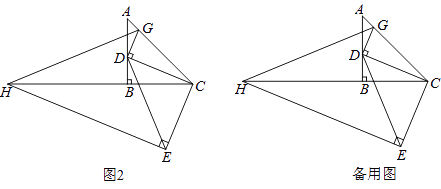
(1)、如图1，作EF⊥BC于F，求证：△DBC≌△CFE；
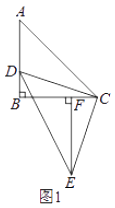(2)、在图1中，连接AE交BC于M，求 的值；
(3)、如图2，过点E作EH⊥CE交CB的延长线于点H，过点D作DG⊥DC，交AC于点G，连接GH．当点D在边AB上运动时，式子 的值会发生变化吗？若不变，求出该值；若变化请说明理由．
