2015-2016学年北京市海淀区八年级上学期期末数学试卷

试卷更新日期：2016-11-28 类型：期末考试

进入出卷网下载

一、选择题

1. 下列标志是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. PM2.5是指大气中直径小于或等于2.5微米的颗粒物，2.5微米等于0.000 002 5米，把数字0.000 002 5用科学记数法表示为（）

A、2.5×10⁶ B、0.25×10^﹣⁶ C、25×10^﹣⁶ D、2.5×10^﹣⁶

查看试题解析
3. 使分式 $\frac{2}{x - 3}$ 有意义的x的取值范围是（）

A、x≠3 B、x＞3 C、x＜3 D、x=3

查看试题解析
4. 下列计算中，正确的是（）

A、（a²）³=a⁸ B、a⁸÷a⁴=a² C、a³+a²=a⁵ D、a²•a³=a⁵

查看试题解析
5. 如图，△ABC≌△DCB，若AC=7，BE=5，则DE的长为（）

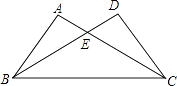A、2 B、3 C、4 D、5

查看试题解析
6. 在平面直角坐标系中，已知点A（2，m）和点B（n，﹣3）关于x轴对称，则m+n的值是（）

A、﹣1 B、1 C、5 D、﹣5

查看试题解析
7. 工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与点M，N重合，过角尺顶点C作射线OC．由此作法便可得△MOC≌△NOC，其依据是（）

A、SSS B、SAS C、ASA D、AAS

查看试题解析
8. 下列各式中，计算正确的是（）

A、x（2x﹣1）=2x²﹣1 B、 $\frac{x + 3}{x^{2} - 9}$ = $\frac{1}{x - 3}$ C、（a+2）²=a²+4 D、（x+2）（x﹣3）=x²+x﹣6

查看试题解析
9. 若a+b=1，则a²﹣b²+2b的值为（）

A、4 B、3 C、1 D、0

查看试题解析
10. 如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线MN交AC于D点，则∠DBC的度数是（）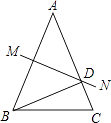

A、20° B、30° C、40° D、50°

查看试题解析
11. 若分式 $\frac{6}{a + 1}$ 的值为正整数，则整数a的值有（）

A、3个 B、4个 C、6个 D、8个

查看试题解析
12.
如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（　　）

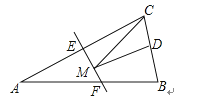A、6 B、8 C、10 D、12

查看试题解析

二、填空题

13. 当x=时，分式 $\frac{x}{x - 1}$ 值为0．

查看试题解析
14. 分解因式：x²y﹣4y= ．

查看试题解析
15. 计算： ${(- \frac{x}{3 y^{2}})}^{2}$ = ．

查看试题解析
16. 已知等腰三角形的两条边长分别为3和7，那么它的周长等于．

查看试题解析
17. 如图，DE⊥AB，∠A=25°，∠D=45°，则∠ACB的度数为．

查看试题解析
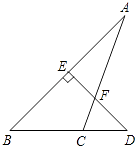18. 等式（a+b）²=a²+b²成立的条件为

查看试题解析
19. 如图，在△ABC中，BD是边AC上的高，CE平分∠ACB，交BD于点E，DE=2，BC=5，则△BCE的面积为．

查看试题解析
20. 图1是用绳索织成的一片网的一部分，小明探索这片网的结点数（V），网眼数（F），边数（E）之间的关系，他采用由特殊到一般的方法进行探索，列表如下：
特殊网图
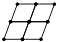
结点数（V）
4
6
9
12
网眼数（F）
1
2
4
6
边数（E）
4
7
12
☆
表中“☆”处应填的数字为；根据上述探索过程，可以猜想V，F，E之间满足的等量关系为；
如图2，若网眼形状为六边形，则V，F，E之间满足的等量关系为．

查看试题解析

三、解答题

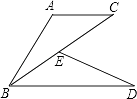
21. 计算： $\sqrt{4}$ ﹣（π﹣3）⁰﹣（ $\frac{1}{2}$ ）^﹣¹+|﹣3|．

查看试题解析
22. 已知：如图，E为BC上一点，AC∥BD，AC=BE，BC=BD．
求证：AB=DE．

查看试题解析
23. 计算： $(\frac{3 x + 4}{x^{2} - 1} - \frac{2}{x - 1}) \div \frac{x + 2}{x^{2} - 2 x + 1}$ ．

查看试题解析
24. 解方程： $\frac{x}{x - 1} - 1 = \frac{3}{x + 1}$ ．

查看试题解析

四、解答题

25. 已知x﹣y=3，求[（x﹣y）²+（x+y）（x﹣y）]÷2x的值．

查看试题解析
26. 北京时间2015年7月31日，国际奥委会主席巴赫宣布：中国北京获得2022年第24届冬季奥林匹克运动会举办权．北京也创造历史，成为第一个既举办过夏奥会又举办冬奥会的城市，张家口也成为本届冬奥会的协办城市．近期，新建北京至张家口铁路可行性研究报告已经获得国家发改委批复，同意新建北京至张家口铁路，铁路全长约180千米．按照设计，京张高铁列车的平均行驶速度是普通快车的1.5倍，用时比普通快车用时少了20分钟，求高铁列车的平均行驶速度．

查看试题解析
27. 已知：如图，线段AB和射线BM交于点B．

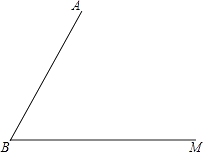(1)、利用尺规完成以下作图，并保留作图痕迹（不写作法）．
①在射线BM上作一点C，使AC=AB；
②作∠ABM的角平分线交AC于D点；
③在射线CM上作一点E，使CE=CD，连接DE．

(2)、在（1）所作的图形中，猜想线段BD与DE的数量关系，并证明．

查看试题解析

五、解答题

28. 如图1，我们在2016年1月的日历中标出一个十字星，并计算它的“十字差”（将十字星左右两数，上下两数分别相乘再将所得的积作差，称为该十字星的“十字差”）．该十字星的十字差为12×14﹣6×20=48，再选择其它位置的十字星，可以发现“十字差”仍为48．

(1)、如图2，将正整数依次填入5列的长方形数表中，探究不同位置十字星的“十字差”，可以发现相应的“十字差”也是一个定值，则这个定值为．

(2)、若将正整数依次填入k列的长方形数表中（k≥3），继续前面的探究，可以发现相应“十字差”为与列数k有关的定值，请用k表示出这个定值，并证明你的结论．

(3)、如图3，将正整数依次填入三角形的数表中，探究不同十字星的“十字差”，若某个十字星中心的数在第32行，且其相应的“十字差”为2015，则这个十字星中心的数为（直接写出结果）．

查看试题解析
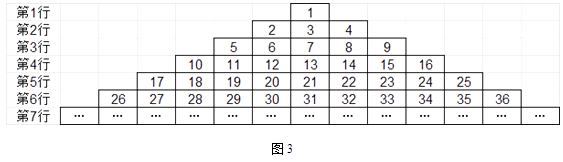29.
数学老师布置了这样一道作业题：
在△ABC中，AB=AC≠BC，点D和点A在直线BC的同侧，BD=BC，∠BAC=α，∠DBC=β，α+β=120°，连接AD，求∠ADB的度数．
小聪提供了研究这个问题的过程和思路：先从特殊问题开始研究，当α=90°，β=30°时（如图1），利用轴对称知识，以AB为对称轴构造△ABD的轴对称图形△ABD′，连接CD′（如图2），然后利用α=90°，β=30°以及等边三角形的相关知识便可解决这个问题．

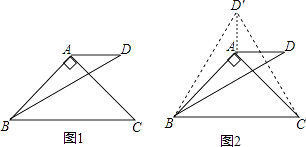(1)、请结合小聪研究问题的过程和思路，求出这种特殊情况下∠ADB的度数；

(2)、结合小聪研究特殊问题的启发，请解决数学老师布置的这道作业题；

(3)、解决完老师布置的这道作业题后，小聪进一步思考，当点D和点A在直线BC的异侧时，且∠ADB的度数与（1）中相同，则α，β满足的条件为（直接写出结果）．

查看试题解析

特殊网图
结点数（V）	4	6	9	12
网眼数（F）	1	2	4	6
边数（E）	4	7	12	☆