四川省资阳市简阳市养马学区2016-2017学年八年级下学期数学期中考试试卷
试卷更新日期:2018-03-30 类型:期中考试
一、单选题
-
1. 在式子 、 、 、 中,分式的个数是( )A、1个 B、2个 C、3个 D、4个2. H7N9禽流感病毒的直径大约是0.000 000 076米,用科学记数法可表示为( )米.
A、7.6×10﹣11 B、7.6×10﹣8 C、7.6×10﹣9 D、7.6×10﹣53. 点P(﹣2,3)关于y轴对称点的坐标是( )A、(﹣2,3) B、(2,﹣3) C、(2,3) D、(﹣2,﹣3)4. 若把一次函数y=2x﹣3,向下平移3个单位长度,得到图象解析式是( )
A、y=2x B、y=2x﹣6 C、y=5x﹣3 D、y=﹣x﹣35. 当k>0,b>0时,一次函数y=kx+b的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 下列图形中的图象不表示y是x的函数的是( )A、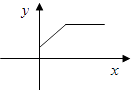 B、
B、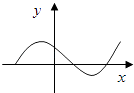 C、
C、 D、
D、 7. 三角形面积为7cm2 , 底边上的高y(cm)与底边x(cm)之间的函数关系的图象大致是( )A、
7. 三角形面积为7cm2 , 底边上的高y(cm)与底边x(cm)之间的函数关系的图象大致是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,点A,B是双曲线y= 上的点,分别经过A,B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=( )
8. 如图,点A,B是双曲线y= 上的点,分别经过A,B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=( )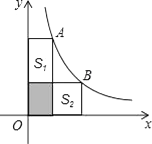 A、2 B、3 C、4 D、59. 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )
A、2 B、3 C、4 D、59. 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( ) A、乙比甲先到达B地 B、乙在行驶过程中没有追上甲 C、乙比甲早出发半小时 D、甲的行驶速度比乙的行驶速度快10. 如图,函数y=k(x+1)与y= 在同一坐标系中,图象只能是下图中的( )A、
A、乙比甲先到达B地 B、乙在行驶过程中没有追上甲 C、乙比甲早出发半小时 D、甲的行驶速度比乙的行驶速度快10. 如图,函数y=k(x+1)与y= 在同一坐标系中,图象只能是下图中的( )A、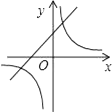 B、
B、 C、
C、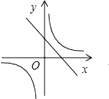 D、
D、
二、填空题
-
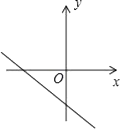
11. 当x=时,分式 的值为0.12. 计算:( )﹣2+( )0= .13. 直线y=(2﹣a)x+3﹣a在直角坐标系中的图象如图所示,化简|3﹣a|+|2﹣a|= .
 14. 如图,反比例函数y= 的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于个面积单位.
14. 如图,反比例函数y= 的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于个面积单位.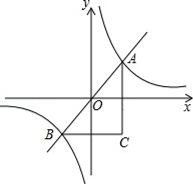 15. 如图为直线y=ax+b的图象,则不等式ax+b<﹣1的解集为 .
15. 如图为直线y=ax+b的图象,则不等式ax+b<﹣1的解集为 . 16. 如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l2于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 .
16. 如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l2于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 .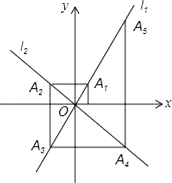
三、解答题
-
17. 计算
(1)、(﹣ )• ;(2)、(a﹣ )÷ .18. 解方程:
(1)、 ;(2)、 .19. 当k为何值时,分式方程 有增根?20. 已知:一次函数的图象与直线y=﹣2x+1平行,且过点(3,2),求此一次函数的解析式.21. 某工厂准备加工600个零件,在加工了100个零件后,采取了新技术,使每天的工作效率是原来的2倍,结果共用7天完成了任务,求该厂原来每天加工多少个零件?
22. 化简 • ﹣ ,并求值,其中a与2、3构成△ABC的三边,且a为整数.23. 4月20日8时2分,四川省雅安市芦山县发生了7.0级地震,当地的部分房屋严重受损,上万灾民无家可归,灾情牵动亿万中国人的心.某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:车 型
运往地
甲 地(元/辆)
乙 地(元/辆)
大货车
720
800
小货车
500
650
(1)、求这两种货车各用多少辆?(2)、如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)、在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
24. 如图,直线l1 , l2交于点A,直线l2与x轴、y轴分别交于点B(﹣4,0)、D(0,4),直线l1所对应的函数关系式为y=﹣2x﹣2.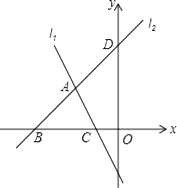 (1)、求点C的坐标及直线l2所对应的函数关系式;(2)、求△ABC的面积;(3)、P是线段BD上的一个动点(点P与B、D不重合).设点P的坐标为(m,n),△PBC的面积为S,写出S与m的函数关系式及自变量m的取值范围.
(1)、求点C的坐标及直线l2所对应的函数关系式;(2)、求△ABC的面积;(3)、P是线段BD上的一个动点(点P与B、D不重合).设点P的坐标为(m,n),△PBC的面积为S,写出S与m的函数关系式及自变量m的取值范围.