广东省深圳市2018年中考数学二模复习卷(一)
试卷更新日期:2018-03-30 类型:中考模拟
一、选择题
-
1. 在﹣2,﹣5,5,0这四个数中,最小的数是( )A、﹣2 B、﹣5 C、5 D、02. 据统计2014年我国高新技术产品出口总额40570亿元,将数据40570亿用科学记数法表示为( )A、4.0570×109 B、0.40570×1010 C、40.570×1011 D、4.0570×10123. 如图,直线l1∥l2 , CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
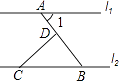 A、50° B、45° C、40° D、30°4. 如图所示的由六个小正方体组成的几何体的俯视图是( )
A、50° B、45° C、40° D、30°4. 如图所示的由六个小正方体组成的几何体的俯视图是( )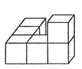 A、
A、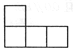 B、
B、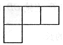 C、
C、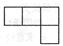 D、
D、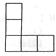 5. 如图,将矩形纸片ABCD沿EF折叠(E,F分别是AD、BC上的点),使点B与四边形CDEF内一点 重合,若 °,则 等于( )
5. 如图,将矩形纸片ABCD沿EF折叠(E,F分别是AD、BC上的点),使点B与四边形CDEF内一点 重合,若 °,则 等于( ) A、110° B、115° C、120° D、130°6. 如图,DE∥BC,分别交△ABC的边AB、AC于点D,E, , 若AE=1,则EC=( ).
A、110° B、115° C、120° D、130°6. 如图,DE∥BC,分别交△ABC的边AB、AC于点D,E, , 若AE=1,则EC=( ).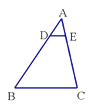 A、2 B、3 C、4 D、67. 将抛物线 向左平移3个单位得到的抛物线的解析式是( )A、 B、 C、 D、8. 甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留),前往终点B地,甲、乙两车之间的距离S(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.下列说法:
A、2 B、3 C、4 D、67. 将抛物线 向左平移3个单位得到的抛物线的解析式是( )A、 B、 C、 D、8. 甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留),前往终点B地,甲、乙两车之间的距离S(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.下列说法:①甲、乙两地相距210千米;②甲速度为60千米/小时;③乙速度为120千米/小时;④乙车共行驶3 小时,其中正确的个数为( )
 A、1个 B、2个 C、3个 D、4个9. 如图,在△ABC中,AB=5,AC=4,BC=3,分别以点A,点B为圆心,大于 AB的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则CO的长是( )
A、1个 B、2个 C、3个 D、4个9. 如图,在△ABC中,AB=5,AC=4,BC=3,分别以点A,点B为圆心,大于 AB的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则CO的长是( )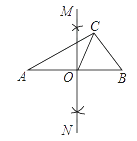 A、1.5 B、2 C、2.4 D、2.510. 某校管乐队购进一批小号和长笛,小号的单价比长笛的单价多100元,用6000元购买小号的数量与用5000元购买长笛的数量恰好相同,设小号的单价为x元,则下列方程正确的是( )A、 B、 C、 D、11. 如图,在射线AB上顺次取两点C,D,使AC=CD=1,以CD为边作矩形CDEF,DE=2,将射线AB绕点A沿逆时针方向旋转,旋转角记为α(其中0°<α<45°),旋转后记作射线AB′,射线AB′分别交矩形CDEF的边CF,DE于点G,H.若CG=x,EH=y,则下列函数图象中,能反映y与x之间关系的是( )
A、1.5 B、2 C、2.4 D、2.510. 某校管乐队购进一批小号和长笛,小号的单价比长笛的单价多100元,用6000元购买小号的数量与用5000元购买长笛的数量恰好相同,设小号的单价为x元,则下列方程正确的是( )A、 B、 C、 D、11. 如图,在射线AB上顺次取两点C,D,使AC=CD=1,以CD为边作矩形CDEF,DE=2,将射线AB绕点A沿逆时针方向旋转,旋转角记为α(其中0°<α<45°),旋转后记作射线AB′,射线AB′分别交矩形CDEF的边CF,DE于点G,H.若CG=x,EH=y,则下列函数图象中,能反映y与x之间关系的是( ) A、
A、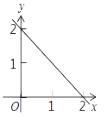 B、
B、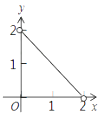 C、
C、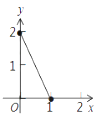 D、
D、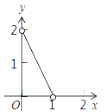 12. ,函数 与 在同一直角坐标系中的大致图象可能是( )A、
12. ,函数 与 在同一直角坐标系中的大致图象可能是( )A、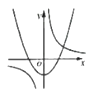 B、
B、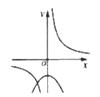 C、
C、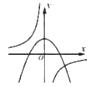 D、
D、
二、填空题
-
13. 分解因式: .14. 如图, 中,∠C=90°, ,则 .
 15. 如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是°.
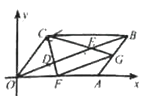
15. 如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是°.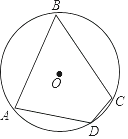 16. 如图,平面直角坐标系中 是原点, 的顶点 的坐标分别是 ,点 把线段 三等分,延长 分别交 于点 ,连接 ,则下列结论:
16. 如图,平面直角坐标系中 是原点, 的顶点 的坐标分别是 ,点 把线段 三等分,延长 分别交 于点 ,连接 ,则下列结论:① 是 的中点;② 与 相似;③四边形 的面积是 ;④ ;其中正确的结论是 . (填写所有正确结论的序号)
三、解答题
-
17. 计算:(1)、2-1+sin30°-|-2|;(2)、(-1)0-|3-π|+ .18. 先化简,再求值: ,其中a= .19. 随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
 (1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?(4)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.20. 如图,直线y=3x与双曲线y= (k≠0,且x>0)交于点A,点A的横坐标是1.
(1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?(4)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.20. 如图,直线y=3x与双曲线y= (k≠0,且x>0)交于点A,点A的横坐标是1.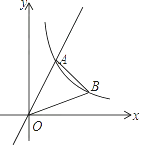 (1)、求点A的坐标及双曲线的解析式;(2)、点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.21. 甲乙两个施工队在六安(六盘水——安顺)城际高铁施工中,每天甲队比乙队多铺设100米钢轨,甲队铺设5天的距离刚好等于乙队铺设6天的距离,若设甲队每天铺设x米,乙队每天铺设y米.(1)、依题意列出二元一次方程组;(2)、求出甲乙两施工队每天各铺设多少米?22. 如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)、求点A的坐标及双曲线的解析式;(2)、点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.21. 甲乙两个施工队在六安(六盘水——安顺)城际高铁施工中,每天甲队比乙队多铺设100米钢轨,甲队铺设5天的距离刚好等于乙队铺设6天的距离,若设甲队每天铺设x米,乙队每天铺设y米.(1)、依题意列出二元一次方程组;(2)、求出甲乙两施工队每天各铺设多少米?22. 如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.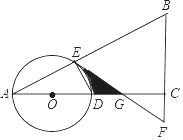 (1)、试判断直线EF与⊙O的位置关系,并说明理由;(2)、若OA=2,∠A=30°,求图中阴影部分的面积.23. 已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.
(1)、试判断直线EF与⊙O的位置关系,并说明理由;(2)、若OA=2,∠A=30°,求图中阴影部分的面积.23. 已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.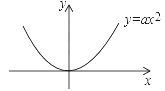 (1)、若∠AOB=60°,AB∥x轴,AB=2,求a的值;(2)、若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;(3)、延长AD、BO相交于点E,求证:DE=CO.
(1)、若∠AOB=60°,AB∥x轴,AB=2,求a的值;(2)、若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;(3)、延长AD、BO相交于点E,求证:DE=CO.