2016年江苏省宿迁市中考数学试卷
试卷更新日期:2016-11-25 类型:中考真卷
一、选择题(本大题共8小题,每小题3分,共24分.在每小题所给出的四个选项中,有且仅有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
-
1. ﹣2的绝对值是( )A、﹣2 B、﹣ C、 D、2
-
2. 下列四个几何体中,左视图为圆的几何体是( )A、
 B、
B、 C、
C、 D、
D、
-
3. 地球与月球的平均距离为384 000km,将384 000这个数用科学记数法表示为( )A、3.84×103 B、3.84×104 C、3.84×105 D、3.84×106
-
4. 下列计算正确的是( )A、a2+a3=a5 B、a2•a3=a6 C、(a2)3=a5 D、a5÷a2=a3
-
5. 如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
 A、50° B、60° C、120° D、130°
A、50° B、60° C、120° D、130° -
6. 一组数据5,4,2,5,6的中位数是( )A、5 B、4 C、2 D、6
-
7. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
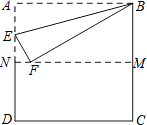 A、2 B、 C、 D、1
A、2 B、 C、 D、1 -
8. 若二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),则方程ax2﹣2ax+c=0的解为( )A、x1=﹣3,x2=﹣1 B、x1=1,x2=3 C、x1=﹣1,x2=3 D、x1=﹣3,x2=1
二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
-
9. 因式分解:2a2﹣8= .
-
10. 计算: = .
-
11. 若两个相似三角形的面积比为1:4,则这两个相似三角形的周长比是 .
-
12. 若一元二次方程x2﹣2x+k=0有两个不相等的实数根,则k的取值范围是 .
-
13. 某种油菜籽在相同条件下发芽试验的结果如表:
每批粒数n
100
300
400
600
1000
2000
3000
发芽的频数m
96
284
380
571
948
1902
2848
发芽的频率
0.960
0.947
0.950
0.952
0.948
0.951
0.949
那么这种油菜籽发芽的概率是(结果精确到0.01).
-
14. 如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为 .

-
15. 如图,在平面直角坐标系中,一条直线与反比例函数y= (x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y= (x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为 .

-
16. 如图,在矩形ABCD中,AD=4,点P是直线AD上一动点,若满足△PBC是等腰三角形的点P有且只有3个,则AB的长为 .

三、解答题(本大题共10题,共72分,请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
-
17. 计算:2sin30°+3﹣1+( ﹣1)0﹣ .
-
18. 解不等式组: .
-
19. 某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
各年级学生成绩统计表
优秀
良好
合格
不合格
七年级
a
20
24
8
八年级
29
13
13
5
九年级
24
b
14
7
根据以上信息解决下列问题:
 (1)、在统计表中,a的值为 , b的值为;(2)、在扇形统计图中,八年级所对应的扇形圆心角为度;(3)、若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数.
(1)、在统计表中,a的值为 , b的值为;(2)、在扇形统计图中,八年级所对应的扇形圆心角为度;(3)、若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数. -
20. 在一只不透明的袋子中装有2个白球和2个黑球,这些球除颜色外都相同.(1)、若先从袋子中拿走m个白球,这时从袋子中随机摸出一个球是黑球的事件为“必然事件”,则m的值为;(2)、若将袋子中的球搅匀后随机摸出1个球(不放回),再从袋中余下的3个球中随机摸出1个球,求两次摸到的球颜色相同的概率.
-
21. 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.

-
22. 如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据: ≈1.73)

-
23. 如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.
 (1)、求证:AC是⊙O的切线;(2)、当BD是⊙O的直径时(如图2),求∠CAD的度数.
(1)、求证:AC是⊙O的切线;(2)、当BD是⊙O的直径时(如图2),求∠CAD的度数. -
24. 某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.(1)、求y关于x的函数表达式;(2)、景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
-
25.
已知△ABC是等腰直角三角形,AC=BC=2,D是边AB上一动点(A、B两点除外),将△CAD绕点C按逆时针方向旋转角α得到△CEF,其中点E是点A的对应点,点F是点D的对应点.
 (1)、如图1,当α=90°时,G是边AB上一点,且BG=AD,连接GF.求证:GF∥AC;(2)、如图2,当90°≤α≤180°时,AE与DF相交于点M.
(1)、如图1,当α=90°时,G是边AB上一点,且BG=AD,连接GF.求证:GF∥AC;(2)、如图2,当90°≤α≤180°时,AE与DF相交于点M.①当点M与点C、D不重合时,连接CM,求∠CMD的度数;
②设D为边AB的中点,当α从90°变化到180°时,求点M运动的路径长.
-
26.
如图,在平面直角坐标系xOy中,将二次函数y=x2﹣1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
 (1)、求N的函数表达式;(2)、设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值;(3)、若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
(1)、求N的函数表达式;(2)、设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值;(3)、若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
