2016年湖南省益阳市中考数学试卷
试卷更新日期:2016-11-25 类型:中考真卷
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 的相反数是( )A、2016 B、﹣2016 C、 D、2. 下列运算正确的是( )A、2x+y=2xy B、x•2y2=2xy2 C、2x÷x2=2x D、4x﹣5x=﹣13. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、两条对角线垂直且平分的四边形是正方形5. 小军为了了解本校运动员百米短跑所用步数的情况,对校运会中百米短跑决赛的8名男运动员的步数进行了统计,记录的数据如下:66、68、67、68、67、69、68、71,这组数据的众数和中位数分别为( )A、67、68 B、67、67 C、68、68 D、68、676. 将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、360° B、540° C、720° D、900°7. 关于抛物线y=x2﹣2x+1,下列说法错误的是( )A、开口向上 B、与x轴有两个重合的交点 C、对称轴是直线x=1 D、当x>1时,y随x的增大而减小8. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
4. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、两条对角线垂直且平分的四边形是正方形5. 小军为了了解本校运动员百米短跑所用步数的情况,对校运会中百米短跑决赛的8名男运动员的步数进行了统计,记录的数据如下:66、68、67、68、67、69、68、71,这组数据的众数和中位数分别为( )A、67、68 B、67、67 C、68、68 D、68、676. 将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、360° B、540° C、720° D、900°7. 关于抛物线y=x2﹣2x+1,下列说法错误的是( )A、开口向上 B、与x轴有两个重合的交点 C、对称轴是直线x=1 D、当x>1时,y随x的增大而减小8. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )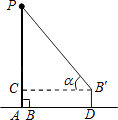 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,每小题5分,共30分.把答案填在答题卡中对应题号后的横线上)
-
9. 将正比例函数y=2x的图象向上平移3个单位,所得的直线不经过第象限.10. 某学习小组为了探究函数y=x2﹣|x|的图象和性质,根据以往学习函数的经验,列表确定了该函数图象上一些点的坐标,表格中的m= .
x
…
﹣2
﹣1.5
﹣1
﹣0.5
0
0.5
1
1.5
2
…
y
…
2
0.75
0
﹣0.25
0
﹣0.25
0
m
2
…
11. 我们把直角坐标系中横坐标与纵坐标都是整数的点称为整点.反比例函数y=﹣ 的图象上有一些整点,请写出其中一个整点的坐标 .12. 如图是一个圆柱体的三视图,由图中数据计算此圆柱体的侧面积为 . (结果保留π) 13. 如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为 .
13. 如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为 . 14.
14.小李用围棋子排成下列一组有规律的图案,其中第1个图案有1枚棋子,第2个图案有3枚棋子,第3个图案有4枚棋子,第4个图案有6枚棋子,…,那么第9个图案的棋子数是枚.
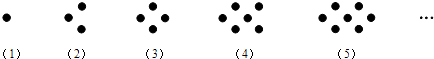
三、解答题(本大题共3小题,每小题8分,共24分)
-
15. 计算:(﹣1)3+| |﹣(﹣ )0×(﹣ ).16. 先化简,再求值:( ﹣ )÷ ,其中x=﹣ .17. 如图,在▱ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.

四、解答题(本大题共3小题,每小题10分,共30分)
-
18. 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组
频数
频率
第一组(0≤x<15)
3
0.15
第二组(15≤x<30)
6
a
第三组(30≤x<45)
7
0.35
第四组(45≤x<60)
b
0.20
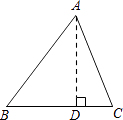
 (1)、频数分布表中a= , b= , 并将统计图补充完整;(2)、如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?(3)、已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?19. 某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.(1)、该班男生和女生各有多少人?(2)、某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?20. 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
(1)、频数分布表中a= , b= , 并将统计图补充完整;(2)、如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?(3)、已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?19. 某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.(1)、该班男生和女生各有多少人?(2)、某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?20. 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.

五、解答题(本题满分12分)
-
21.
如图,顶点为A( ,1)的抛物线经过坐标原点O,与x轴交于点B.
 (1)、求抛物线对应的二次函数的表达式;(2)、过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;(3)、在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
(1)、求抛物线对应的二次函数的表达式;(2)、过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;(3)、在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.六、解答题(本题满分14分)
-
22. 如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
 (1)、计算矩形EFGH的面积;(2)、将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为 时,求矩形平移的距离;(3)、如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1 , 将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2 , 设旋转角为α,求cosα的值.
(1)、计算矩形EFGH的面积;(2)、将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为 时,求矩形平移的距离;(3)、如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1 , 将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2 , 设旋转角为α,求cosα的值.
-