2016年湖南省怀化市中考数学试卷
试卷更新日期：2016-11-25 类型：中考真卷
一、选择题：每小题4分，共40分
-
1. （﹣2）2的平方根是（ ）A、2 B、﹣2 C、±2 D、2. 某校进行书法比赛，有39名同学参加预赛，只能有19名同学参加决赛，他们预赛的成绩各不相同，其中一名同学想知道自己能否进入决赛，不仅要了解自己的预赛成绩，还要了解这39名同学预赛成绩的（ ）A、平均数 B、中位数 C、方差 D、众数3. 下列计算正确的是（ ）A、（x+y）2=x2+y2 B、（x﹣y）2=x2﹣2xy﹣y2 C、（x+1）（x﹣1）=x2﹣1 D、（x﹣1）2=x2﹣14. 一元二次方程x2﹣x﹣1=0的根的情况为（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C，D，则下列结论错误的是（ ）
A、PC=PD B、∠CPD=∠DOP C、∠CPO=∠DPO D、OC=OD6. 不等式3（x﹣1）≤5﹣x的非负整数解有（ ）A、1个 B、2个 C、3个 D、4个7. 二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是（ ）A、开口向上，顶点坐标为（﹣1，﹣4） B、开口向下，顶点坐标为（1，4） C、开口向上，顶点坐标为（1，4） D、开口向下，顶点坐标为（﹣1，﹣4）8. 等腰三角形的两边长分别为4cm和8cm，则它的周长为（ ）A、16cm B、17cm C、20cm D、16cm或20cm9. 函数y= 中，自变量x的取值范围是（ ）A、x≥1 B、x＞1 C、x≥1且x≠2 D、x≠210. 在Rt△ABC中，∠C=90°，sinA= ，AC=6cm，则BC的长度为（ ）A、6cm B、7cm C、8cm D、9cm二、填空题：本大题共4小题，每小题4分，共16分
-
11. 已知扇形的半径为6cm，面积为10πcm2 ， 则该扇形的弧长等于cm．12. 旋转不改变图形的和 ．13. 已知点P（3，﹣2）在反比例函数y= （k≠0）的图象上，则k=；在第四象限，函数值y随x的增大而 ．14. 一个不透明的袋子，装了除颜色不同，其他没有任何区别的红色球3个，绿色球4个，黑色球7个，黄色球2个，从袋子中随机摸出一个球，摸到黑色球的概率是 ．
三、解答题：本大题共8小题，每小题8分，共64分
-
15. 计算：20160+2|1﹣sin30°|﹣（ ）﹣1+ ．16. 有若干只鸡和兔关在一个笼子里，从上面数，有30个头；从下面数，有84条腿，问笼中各有几只鸡和兔？17. 如图，已知AD=BC，AC=BD．
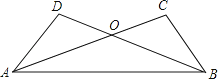(1)、求证：△ADB≌△BCA；(2)、OA与OB相等吗？若相等，请说明理由．18. 已知一次函数y=2x+4
(1)、在如图所示的平面直角坐标系中，画出函数的图象；(2)、求图象与x轴的交点A的坐标，与y轴交点B的坐标；(3)、在（2）的条件下，求出△AOB的面积；(4)、利用图象直接写出：当y＜0时，x的取值范围．19. 如图，在Rt△ABC中，∠BAC=90°
(1)、先作∠ACB的平分线交AB边于点P，再以点P为圆心，PA长为半径作⊙P；（要求：尺规作图，保留作图痕迹，不写作法）(2)、请你判断（1）中BC与⊙P的位置关系，并证明你的结论．20. 甲、乙两人都握有分别标记为A、B、C的三张牌，两人做游戏，游戏规则是：若两人出的牌不同，则A胜B，B胜C，C胜A；若两人出的牌相同，则为平局．(1)、用树状图或列表等方法，列出甲、乙两人一次游戏的所有可能的结果；(2)、求出现平局的概率．21. 如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm．
(1)、求证：△AEH∽△ABC；(2)、求这个正方形的边长与面积．22.如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣3，0）、B（5，0）、C（0，5）三点，O为坐标原点
(1)、求此抛物线的解析式；(2)、若把抛物线y=ax2+bx+c（a≠0）向下平移 个单位长度，再向右平移n（n＞0）个单位长度得到新抛物线，若新抛物线的顶点M在△ABC内，求n的取值范围；(3)、设点P在y轴上，且满足∠OPA+∠OCA=∠CBA，求CP的长．