2018年中考数学几何部分基础考点训练10：平行四边形
试卷更新日期：2018-03-27 类型：一轮复习
一、单选题
-
1. 四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD，从中任选两个条件，能使四边形ABCD为平行四边形的选法有（ ）．A、3种 B、4种 C、5种 D、6种2. 能判定四边形ABCD为平行四边形的题设是（）．A、AB∥CD，AD＝BC B、∠A＝∠B，∠C＝∠D C、AB＝CD，AD＝BC D、AB＝AD，CB＝CD3. 下面给出四边形ABCD中，∠A ， ∠B ， ∠C ， ∠D的度数之比，其中能判定四边形ABCD为平行四边形的是（ ）A、1∶2∶3∶4 B、2∶3∶2∶3 C、2∶2∶3∶3 D、1∶2∶2∶3
二、解答题
-
4. 如图，在▱ABCD中，∠ADC的平分线交AB于点E，∠ABC的平分线交CD于点F，求证：四边形EBFD是平行四边形．
5. 如图，在▱ABCD中，F是AD的中点，延长BC到点E，使CE= BC，连接DE，CF．求证：四边形CEDF是平行四边形．
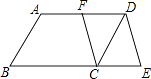6. 如图，在平行四边形ABCD中，已知点E在AB上，点F在CD上，且AE=CF．求证：DE=BF．
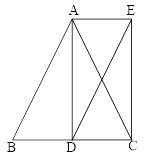
7.如图，在△ABC中，AB=AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为点E.连接DE， 则线段DE与线段AC有怎样的数量关系？请证明你的结论。
8.如图，平行四边形ABCD中，点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG，AH=CF．
（1）求证：四边形EFGH是平行四边形；
（2）如果AB=AD，且AH=AE，求证：四边形EFGH是矩形．
9.如图，直线y=x+3与x轴交于点A，与y轴交于点B，抛物线y=﹣x2+bx+c经过A、B两点．
（1）求抛物线的解析式；
（2）点P为抛物线在第二象限内一点，过点P作x轴的垂线，垂足为点M，与直线AB交于点C，过点P作x轴的平行线交抛物线于点Q，过点Q作x轴的垂线，垂足为点N，若点P在点Q左边，设点P的横坐标为m．
①当矩形PQNM的周长最大时，求△ACM的面积；
②在①的条件下，当矩形PMNQ的周长最大时，过直线AC上一点G作y轴的平行线交抛物线一点F，是否存在点F，使得以点P、C、G、F为顶点的四边形是平行四边形？若存在，请直接写出点F的坐标；若不存在，请说明理由．
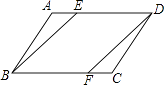
10. 如图，在▱ABCD中，点E、F分别在AD、BC上，且AE=CF．求证：四边形BFDE是平行四边形．
三、填空题
