2018年中考数学几何部分基础考点训练09：三角形
试卷更新日期：2018-03-27 类型：一轮复习
一、单选题
-
1.
如图，在四边形ABCD中，E、F分别是AB、AD的中点，若EF=4，BC=10，CD=6，则tanC等于（ ）
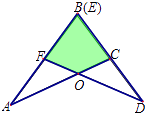
A、 B、 C、 D、2. 如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①、②、③、④四个三角形．若OA：OC=OB：OD，则下列结论中一定正确的是（ ）
A、①与②相似 B、①与③相似 C、①与④相似 D、②与④相似3. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．若AC= ，BC=2，则sin∠ACD的值为（ ）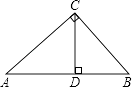
A、 B、 C、 D、二、填空题
-
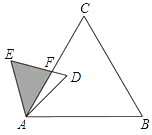
4. 如图，已知△ABC是面积为 的等边三角形，△ABC∽△ADE，AB=2AD，∠BAD=45°，AC与DE相交于点F，则△AEF的面积等于（结果保留根号）．
5.已知：如图，三个半圆依次相外切，它们的圆心都在x轴的正半轴上并与直线y=x相切，设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3 ， 则当r1=1时，r3= ．
6. 如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=5cm，则EF=cm．
7. 如图，在Rt△ABC中，∠ABC=90°，∠ACB=30°．将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1 ， B1C1交AC于点D，如果AD=2 ，则△ABC的周长等于 ．
8. 如图，测量河宽AB（假设河的两岸平行），在C点测得∠ACB=30°，D点测得∠ADB=60°，又CD=60m，则河宽AB为m（结果保留根号）．
三、综合题
-
9. 如图，已知四边形ABCD是梯形，AD∥BC，∠A=90°，BC=BD，CE⊥BD，垂足为E．
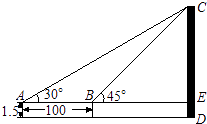
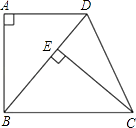(1)、求证：△ABD≌△ECB；(2)、若∠DBC=50°，求∠DCE的度数．10.如图所示，小明在大楼30米高（即PH=30米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1： ，点P、H、B、C、A在同一个平面上．点H、B、C在同一条直线上，且PH⊥HC．
(1)、山坡坡角（即∠ABC）的度数等于度；(2)、求山坡A、B两点间的距离（结果精确到0.1米）．（参考数据： ≈1.414， ≈1.732）
11.如图，自来水厂A和村庄B在小河l的两侧，现要在A，B间铺设一条输水管道．为了搞好工程预算，需测算出A，B间的距离．一小船在点P处测得A在正北方向，B位于南偏东24.5°方向，前行1200m，到达点Q处，测得A位于北偏西49°方向，B位于南偏西41°方向．
(1)、线段BQ与PQ是否相等？请说明理由；(2)、求A，B间的距离．（参考数据cos41°≈0.75）四、解答题
-
12.
如图，一架飞机由A向B沿水平直线方向飞行，在航线AB的正下方有两个山头C、D．飞机在A处时，测得山头C、D在飞机的前方，俯角分别为60°和30°．飞机飞行了6千米到B处时，往后测得山头C的俯角为30°，而山头D恰好在飞机的正下方．求山头C、D之间的距离．
