四川省绵阳市平武县2016届中考数学一模试卷
试卷更新日期:2018-03-26 类型:中考模拟
一、选择题
-
1. 的倒数的相反数是( )A、 B、2 C、﹣2 D、﹣2. 下列运算中,正确的是( )A、2xa+xa=3x2a2 B、(a2)3=a6 C、3a•2a=6a D、3﹣2=﹣63. 下列说法中正确的是( )A、“打开电视,正在播放《新闻联播》”是必然事件 B、想了解某种饮料中含色素的情况,宜采用抽样调查 C、数据1,1,2,2,3的众数是3 D、一组数据的波动越大,方差越小4. 如图是由几块小立方块所搭成的几何体的俯视图,小正方体中的数字表示该位置小立方块的个数,则该几何体的左视图是( )
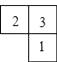 A、
A、 B、
B、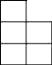 C、
C、 D、
D、 5. 根据以下对话,可以求得小红所买的笔和笔记本的价格分别是( )
5. 根据以下对话,可以求得小红所买的笔和笔记本的价格分别是( )
A、3元、2元 B、2元、3元 C、3.4元、1.6元 D、1.2元、3.6元6. 把分式 中的x、y的值都扩大到原来的2倍,则分式的值( )A、不变 B、扩大到原来的2倍 C、扩大到原来的4倍 D、缩小到原来的7. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是( )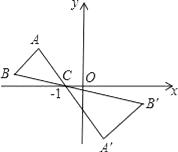 A、3 B、﹣3 C、﹣4 D、48.
A、3 B、﹣3 C、﹣4 D、48.如图,半圆A和半圆B均与y轴相切于O,其直径CD,EF均和x轴垂直,以O为顶点的两条抛物线分别经过点C,E和点D,F,则图中阴影部分面积是( )
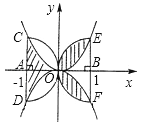 A、π B、π C、π D、条件不足,无法求9. 如图,⊙O内切于△ABC,切点为D,E,F,若∠B=50°,∠C=60°,连接OE,OF,DE,DF,∠EDF等于( )
A、π B、π C、π D、条件不足,无法求9. 如图,⊙O内切于△ABC,切点为D,E,F,若∠B=50°,∠C=60°,连接OE,OF,DE,DF,∠EDF等于( )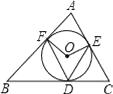 A、45° B、55° C、65° D、70°10. 如图,在Rt△ABC中,∠C=90°,AC= ,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是( )
A、45° B、55° C、65° D、70°10. 如图,在Rt△ABC中,∠C=90°,AC= ,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是( ) A、1 B、 C、 D、11. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论:
A、1 B、 C、 D、11. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论:①当x=3时,y=0;
②3a+b>0;
③﹣1≤a≤﹣ ;
④ ≤n≤4.
其中正确的有( )
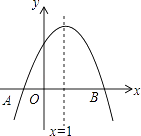 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
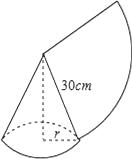
12. 在函数y= +(x﹣1)0中,自变量x的取值范围是 .13. 五张质地、大小、背面完全相同的卡片上,正面分别画有圆、矩形、等边三角形、菱形、平行四边形五个图案,现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为 .14. 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为 .
 15. 菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售,由于部分菜农盲目扩大种植,造成蔬菜滞销,李伟为了加快销售,减少损失,对价格进行两次下调后,以每千克3.2元的单价对外批发销售.平均每次下调的百分率是
15. 菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售,由于部分菜农盲目扩大种植,造成蔬菜滞销,李伟为了加快销售,减少损失,对价格进行两次下调后,以每千克3.2元的单价对外批发销售.平均每次下调的百分率是
16. 已知x1、x2为方程x2+3x+1=0的两实根,则x13+8x2+20= .17. 小数在数学外小组活动中遇到这样一个问题:如果α、β都为锐角,且tanα= ,tanβ= .求α+β的度数.
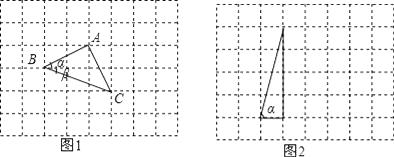 (1)、小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得α+β=∠ABC=°.(2)、请你参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ= 时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β,由此可得α﹣β=°.
(1)、小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得α+β=∠ABC=°.(2)、请你参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ= 时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β,由此可得α﹣β=°.三、解答题
-
18. 解答下面两题,并将结果在数轴上表示出来.(1)、解不等式 并把不等式组的解集在数轴上表示.(2)、解方程 .
 19. 体考在即,初三(1)班的课题研究小组对本年级530名学生的体育达标情况进行调查,制作出如图所示的统计图,其中1班有50人.(注:30分以上为达标,满分50分)根据统计图,解答下面问题:
19. 体考在即,初三(1)班的课题研究小组对本年级530名学生的体育达标情况进行调查,制作出如图所示的统计图,其中1班有50人.(注:30分以上为达标,满分50分)根据统计图,解答下面问题: (1)、初三(1)班学生体育达标率和本年级其余各班学生体育达标率各是多少?(2)、若除初三(1)班外其余班级学生体育考试成绩在30﹣﹣40分的有120人,请补全扇形统计图;(注:请在图中分数段所对应的圆心角的度数)(3)、如果要求全年级学生的体育达标率不低于90%,试问在本次调查中,该年级全体学生的体育达标率是否符合要求?20. 在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2
(1)、初三(1)班学生体育达标率和本年级其余各班学生体育达标率各是多少?(2)、若除初三(1)班外其余班级学生体育考试成绩在30﹣﹣40分的有120人,请补全扇形统计图;(注:请在图中分数段所对应的圆心角的度数)(3)、如果要求全年级学生的体育达标率不低于90%,试问在本次调查中,该年级全体学生的体育达标率是否符合要求?20. 在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2 (1)、求S关于x的函数关系式,并直接写出自变量x的取值范围.(2)、若a=400,求S的最大值,并求出此时x的值.21. 已知关于x的方程kx2+(2k+1)x+2=0.(1)、求证:无论k取任何实数时,方程总有实数根.(2)、是否存在实数k使方程两根的倒数和为2?若存在,请求出k的值;若不存在,请说明理由.22. 如图,反比例函数y= 的图象与二次函数y=﹣x2+bx+c的图象在第一象限内相交A、B两点,A、B两点的纵坐标分别为1,3,且AB=2
(1)、求S关于x的函数关系式,并直接写出自变量x的取值范围.(2)、若a=400,求S的最大值,并求出此时x的值.21. 已知关于x的方程kx2+(2k+1)x+2=0.(1)、求证:无论k取任何实数时,方程总有实数根.(2)、是否存在实数k使方程两根的倒数和为2?若存在,请求出k的值;若不存在,请说明理由.22. 如图,反比例函数y= 的图象与二次函数y=﹣x2+bx+c的图象在第一象限内相交A、B两点,A、B两点的纵坐标分别为1,3,且AB=2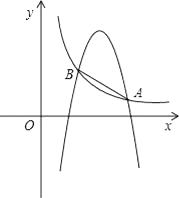 (1)、求反比例函数的解析式;(2)、求二次函数的解析式;(3)、如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.23. 如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.
(1)、求反比例函数的解析式;(2)、求二次函数的解析式;(3)、如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.23. 如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.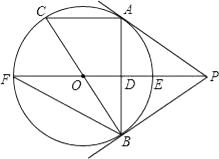 (1)、求证:PB与⊙O相切;(2)、是探究线段EF,OD,OP之间的数量关系,并加以证明;(3)、若tan∠F= ,求cos∠ACB的值.24. 操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.图1,2,3是旋转三角板得到的图形中的3种情况.
(1)、求证:PB与⊙O相切;(2)、是探究线段EF,OD,OP之间的数量关系,并加以证明;(3)、若tan∠F= ,求cos∠ACB的值.24. 操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.图1,2,3是旋转三角板得到的图形中的3种情况.研究:
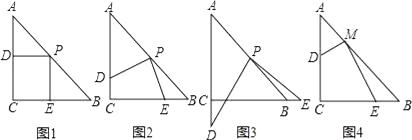 (1)、三角板绕点P旋转,观察线段PD和PE之间有什么数量关系,并结合图2加以证明;(2)、三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由;(3)、若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图4加以证明.
(1)、三角板绕点P旋转,观察线段PD和PE之间有什么数量关系,并结合图2加以证明;(2)、三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由;(3)、若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图4加以证明.