四川省绵阳市平武县2015-2016学年八年级上学期数学期中考试试卷
试卷更新日期：2018-03-26 类型：期中考试
一、选择题．
-
1. 下列图形中对称轴最多的是（ ）A、圆 B、正方形 C、等腰三角形 D、线段2. 下列能组成三角形的线段是（ ）A、3cm、3cm、6cm B、3cm、4cm、5cm C、2cm、4cm、6cm D、3cm、5cm、9cm3. 如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
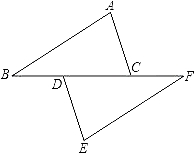
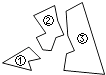A、带①去 B、带②去 C、带③去 D、带①和②去4. 已知：如图，AC=AE，∠1=∠2，AB=AD，若∠D=25°，则∠B的度数为（ ）
A、25° B、30° C、15° D、30°或15°5. 下列说法正确的是（ ）A、等腰三角形的高，中线，角平分线互相重合 B、顶角相等的两个等腰三角形全等 C、面积相等的两个三角形全等 D、等腰三角形的两个底角相等6. 如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（ ）A、锐角三角形 B、钝角三角形 C、直角三角形 D、不能确定7. 课本107页，画∠AOB的角平分线的方法步骤是：①以O为圆心，适当长为半径作弧，交OA于M点，交OB于N点；
②分别以M，N为圆心，大于 MN的长为半径作弧，两弧在∠AOB的内部相交于点C；
③过点C作射线OC．
射线OC就是∠AOB的角平分线．
请你说明这样作角平分线的根据是（ ）
A、SSS B、SAS C、ASA D、AAS8. 如图，把长方形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么，有下列说法：①△EBD是等腰三角形，EB=ED；②折叠后∠ABE和∠CBD一定相等；
③折叠后得到的图形是轴对称图形；
④△EBA和△EDC一定是全等三角形．其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个9. 三角形中，到三个顶点距离相等的点是（ ）A、三条高线的交点 B、三条中线的交点 C、三条角平分线的交点 D、三边垂直平分线的交点10. 如图，AC=DF，∠ACB=∠DFE，下列哪个条件不能判定△ABC≌△DEF（ ）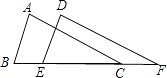
A、∠A=∠D B、BE=CF C、AB=DE D、AB∥DE二、填空题
-
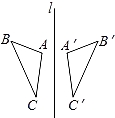
11. 等腰三角形的两边长为4，9．则它的周长为 ．12. 如图，△ABC与△A′B′C′关于直线l对称，且∠A=98°，∠C′=48°，则∠B的度数为 ．
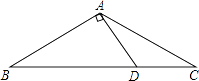
13. 如图：△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，则△ABC的周长为 ．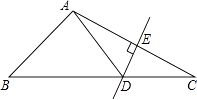
14. 等边△ABC的两条角平分线BD与CE交于点O，则∠BOC等于 ．
15. 已知点P到x轴，y轴的距离分别是2和3，且点P关于y轴对称的点在第四象限，则点P的坐标是 ．16. 如图，在△ABC中，∠C=90°，AE平分∠BAC，CE=6，则点E到AB的距离是 ．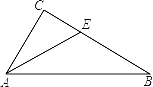
17.一辆汽车的车牌号在水中的倒影是：
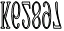那么它的实际车牌号是：18. 如图，∠ADC=°．
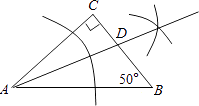19. 正五边形每个内角的度数为 ．
20. 某轮船由西向东航行，在A处测得小岛P的方位是北偏东75°，又继续航行7海里后，在B处测得小岛P的方位是北偏东60°，则此时轮船与小岛P的距离BP=海里．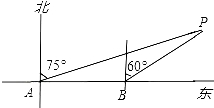
三、解答题
-
21. 如图，A，B是两个蓄水池，都在河流a的同侧，为了方便灌溉作物，要在河边建一个抽水站，将河水送到A，B两地，问该站建在河边什么地方，可使所修的渠道最短，试在图中确定该点．（保留作图痕迹）
22. 如图，在平面直角坐标系XOY中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．
(1)、请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；(2)、直接写出A′，B′，C′三点的坐标：A′（），B′（），C′（）(3)、计算△ABC的面积．
