山东省新泰市2016届九年级上学期学科学习能力成果展示竞赛数学试卷

试卷更新日期：2018-03-26 类型：竞赛测试

进入出卷网下载

一、单选题

1. 已知∠A=65°，则∠A的余角等于（　　）

A、115° B、55° C、35° D、25°

查看试题解析
2. 下列说法中，错误的是（　　）.

A、平行四边形的对角线互相平分 B、对角线互相平分的四边形是平行四边形 C、菱形的对角线互相垂直 D、对角线互相垂直的四边形是菱形

查看试题解析
3. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 在实数π、 $\frac{1}{3}$ 、 $\sqrt{2}$ 、tan60°中，无理数的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 下列运算中，正确的是（）

A、-（m+n）=n-m B、（m³n²）³=m⁶n⁵ C、m³•m²=m⁵ D、n³÷n³=n

查看试题解析
6. 如果 $\sqrt{（ x - 2 ）^{2}}$ ＝2−x，那么x取值范围是（）

A、x≤2 B、x＜2 C、x≥2 D、x＞2

查看试题解析
7. 分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则（）

A、x=-1 B、x=1 C、x=±1 D、x=0

查看试题解析
8.
如图，已知AB∥CD，E是AB上一点，DE平分∠BEC交CD于D，∠C=80°，则∠D的度数是（　　）

A、40° B、45° C、50° D、55°

查看试题解析
9. 小明乘出租车去体育场，有两条路线可供选择：路线一的全程是25千米，但交通比较拥堵，路线二的全程是30千米，平均车速比走路线一时的平均车速能提高80%，因此能比走路线一少用10分钟到达．若设走路线一时的平均速度为x千米/小时，根据题意得：（）

A、 $\frac{25}{x} - \frac{30}{(1 + 80 %) x} = \frac{10}{60}$ B、 $\frac{25}{x} - \frac{30}{(1 + 80 %) x} = 10$ C、 $\frac{30}{(1 + 80 %) x} - \frac{25}{x} = \frac{10}{60}$ D、 $\frac{30}{(1 + 80 %) x} - \frac{25}{x} = 10$

查看试题解析
10. 已知关于 $x$ 的方程 $(2 a + b) x - 1 = 0$ 无解，那么 $a b$ 的值是（）

A、负数 B、正数 C、非负数 D、非正数

查看试题解析
11. 在平面直角坐标系中有两点A（-1，2），B（3，2），若点C是坐标轴上的一点，且△ABC是直角三角形，则满足条件的点C的个数为（）

A、3 B、4 C、5 D、6

查看试题解析
12. 如图，在Rt△ABC中，∠C=90°，AC=BC=6cm，点P从点A出发，沿AB方向以每秒 $\sqrt{2}$ cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿QC翻折，点P的对应点为点P′．设点Q运动的时间为t秒，若四边形QPCP′为菱形，则t的值为（）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、3

查看试题解析
13. 已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B₁在y轴上，点C₁、E₁、E₂、C₂、E₃、E₄、C₃在x轴上．若正方形A₁B₁C₁D₁的边长为1，∠B₁C₁O=60°，B₁C₁∥B₂C₂∥B₃C₃ ，则点A₃到x轴的距离是（）

A、 $\frac{\sqrt{3} + 3}{18}$ B、 $\frac{\sqrt{3} + 1}{18}$ C、 $\frac{\sqrt{3} + 3}{6}$ D、 $\frac{\sqrt{3} + 1}{6}$

查看试题解析
14. 若函数 $y = \frac{1}{2} (x^{2} - 100 x + 196 + | x^{2} - 100 x + 196 |)$ ，则当自变量 $x$ 取1、2、3、…、100这100个自然数时，函数值的和是（）。

A、540 B、390 C、194 D、97

查看试题解析

二、填空题

15. 50名学生中，会讲英语的有36人，会讲日语的有20人，既不会讲英语也不会讲日语的有8人，则既会讲英语又会讲日语的人数为人．

查看试题解析
16. 如图是“横店影视城”的圆弧形门，妙可同学到影视城游玩，很想知道这扇门的相关数据．于是她从景点管理人员处打听到：这个圆弧形门所在的圆与水平地面是相切的， $A B = C D = 20$ cm， $B D = 200$ cm，且 $A B ， C D$ 与水平地面都是垂直的．根据以上数据，你帮助妙可同学计算这个圆弧形门的最高点离地面的高度是．

查看试题解析
17. 我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S₁ ， S₂ ， S₃ ，若S₁+S₂+S₃=10，则S₂的值是．

查看试题解析
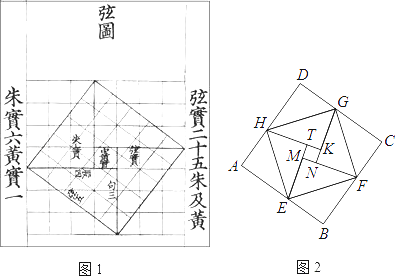18. 如图，在菱形ABCD和菱形BEFG中，点A、B、E在同一直线上，P是线段DF的中点，连接PG，PC．若∠ABC=∠BEF=60°，则 $\frac{P G}{P C}$ = ．

查看试题解析
19. 设n是大于1909的正整数，使得 $\frac{n - 1909}{2009 - n}$ 为完全平方数的n的个数是．

查看试题解析
20. 设a= $\sqrt{7}$ -1，则3a³+12a²-6a-12= ．

查看试题解析
21. 在平面直角坐标系xOy中，对于点P（x，y），我们把点P（﹣y+1，x+1）叫做点P的伴随点．已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得到点A₁ ， A₂ ， A₃ ， …，A_n ， …．若点A₁的坐标为（3，1），则点A₂₀₁₅的坐标为；若点A₁的坐标为（a，b），对于任意的正整数n，点A_n均在x轴上方，则a，b应满足的条件为。

查看试题解析

三、解答题

22. 某人在电车路轨旁与路轨平行的路上骑车行走，他留意到每隔6分钟有一部电车从他后面驶向前面，每隔2分钟有一部电车从对面驶向后面。假设电车和此人行驶的速度都不变（分别为，表示），请你根据下面的示意图，求电车每隔几分钟（用t表示）从车站开出一部？

查看试题解析
23. 如图，AB是⊙O的直径，D为圆周上任一点，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE于点F．

(1)、求证：；

(2)、若，⊙O的半径为3，求BC的长．

查看试题解析
24. 如图1是安装在斜屋面上的太阳能热水器，图2是安装该热水器的侧面示意图．已知，斜屋面的倾角为25°，长为2.1米的真空管AB与水平线AD的夹角为40°，安装热水器的铁架水平横管BC长0.2米，求铁架垂直管CE的长（结果精确到0.01米）．（说明：sin40°≈0.645，cos40°≈0.766，sin25°≈0.423，cos25°≈0.906，tan25°≈0.466。）

查看试题解析
25. 如图所示的一张矩形纸片 $A B C D$ （ $A D > A B$ ），将纸片折叠一次，使点 $A$ 与 $C$ 重合，再展开，折痕 $E F$ 交 $A D$ 边于 $E$ ，交 $B C$ 边于 $F$ ，AC与EF交于点O，分别连结 $A F$ 和 $C E$ ．在线段 $A C$ 上是否存在一点 $P$ ，使得2AE²=AC·AP？若存在，请说明点 $P$ 的位置，并予以证明；若不存在，请说明理由．

查看试题解析
26. 阅读下面材料：
小明遇到这样一个问题：如图1，在边长为 $a (a > 2)$ 的正方形ABCD各边上分别截取AE＝BF＝CG＝DH＝1，当∠AFQ＝∠BGM＝∠CHN＝∠DEP＝45°时，求正方形MNPQ的面积．
小明发现：分别延长QE，MF， NG，PH，交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形（如图2）。请回答：

(1)、若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙，不重叠），则这个新的正方形的边长为；

(2)、求正方形MNPQ的面积．

(3)、参考小明思考问题的方法，解决问题：
如图3，在等边△ABC各边上分别截取AD＝BE＝CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ，若 $S_{Δ R P Q} = \frac{\sqrt{3}}{3}$ ，则AD的长为．

查看试题解析