2010年第十四届华罗庚金杯少年数学邀请赛总决赛试卷
试卷更新日期:2018-03-26 类型:竞赛测试
一、填空题
-
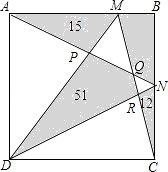
1. 分数 , , , , 中最小的一个是。2. 如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为 .
 3. 将105表示成不少于两个连续的(非零)自然数之和,最多有种表达方式。4. 将奇数1、3、5、…、2007、2009从小到大排成一个多位数A=13579111315…20072009,从A中截出能被5整除的五位数,则所有的这种五位数中,最小数是 , 最大数是。
3. 将105表示成不少于两个连续的(非零)自然数之和,最多有种表达方式。4. 将奇数1、3、5、…、2007、2009从小到大排成一个多位数A=13579111315…20072009,从A中截出能被5整除的五位数,则所有的这种五位数中,最小数是 , 最大数是。
二、解答题
