山东临沂临沭县新华杯2015-2016学年九年级上学期素养展示大赛数学试卷

试卷更新日期：2018-03-23 类型：竞赛测试

进入出卷网下载

一、单选题

1. 已知二次函数y=x²﹣6x+m的最小值是﹣3，那么m的值等于（）

A、10 B、4 C、5 D、6

查看试题解析
2. 在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同．其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
3. 已知命题“关于x的一元二次方程x²+bx+1=0，当b＜0时必有实数解”，能说明这个命题是假命题的一个反例可以是（）

A、b=﹣1 B、b=2 C、b=﹣2 D、b=0

查看试题解析
4. 如图，⊙O是△ABC的外接圆，OD⊥AB于点D，交⊙O于点E，∠C=60°，如果⊙O的半径为2，则结论错误的是（）

A、AD=DB B、 $\hat{A E} = \hat{E B}$ C、OD=1 D、AB= $\sqrt{3}$

查看试题解析
5. 如图，△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为（）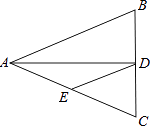

A、20 B、12 C、14 D、13

查看试题解析
6. 如图，▱ABCD的顶点A、B、D在⊙O上，顶点C在⊙O的直径BE上，连接AE，∠E=36°，则∠ADC的度数是（）

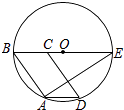A、44° B、54° C、72° D、53°

查看试题解析
7. 已知点P（a，a+3）在抛物线y=x²﹣7x+19图象上，则点P关于原点O的对称点P′的坐标是（）

A、（4，7） B、（﹣4，﹣7） C、（4，﹣7） D、（﹣4，7）

查看试题解析
8. 若A（﹣ $\frac{13}{4}$ ，y₁），B（ $- \frac{5}{4}$ ，y₂），C（ $\frac{1}{4}$ ，y₃）为二次函数y=x²+4x﹣5的图象上的三点，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₃＜y₁＜y₂ D、y₁＜y₃＜y₂

查看试题解析
9. 下列图形中阴影部分面积相等的是（）

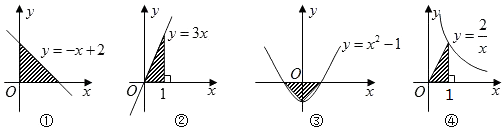A、①② B、②③ C、①④ D、③④

查看试题解析
10. 如图，已知点A，B，C，D，E，F是边长为1的正六边形的顶点，连接任意两点均可得到一条线段．在连接两点所得的所有线段中任取一条线段，取到长度为 $\sqrt{3}$ 的线段的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{2}{5}$ C、 $\frac{2}{3}$ D、 $\frac{5}{9}$

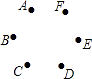查看试题解析
11. 已知二次函数y=ax²+bx+c+2的图象如图，顶点为(-1，0)，下列结论：①abc<0；②b²-4ac=0；③a>2；④4a-2b+c>0.其中正确结论的个数是( )

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，抛物线y=﹣2x²﹣8x﹣6与x轴交于点A，B，把抛物线在x轴及其上方的部分记作C₁ ，将C₁向左平移得C₂ ， C₂与x轴交于点B，D．若直线y=﹣x+m与C₁ ， C₂共有3个不同的交点，则m的取值范围是（）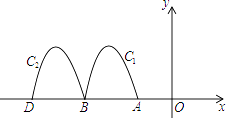

A、﹣3＜m＜﹣ $\frac{15}{8}$ B、 $﹣ 3 < m < ﹣ \frac{7}{4}$ C、﹣2＜m＜ $\frac{1}{8}$ D、﹣3＜m＜﹣2

查看试题解析
13. 如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D，过点C作CF∥AB，在CF上取一点E，使DE=CD，连接AE，对于下列结论：①AD=DC；②△CBA∽△CDE；③ $\hat{B D}$ = $\hat{A D}$ ；④AE为⊙O的切线，一定正确的结论选项是．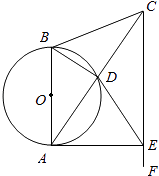

查看试题解析

二、填空题

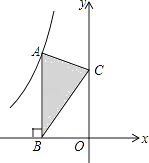
14. 从-2、-1、0、1、2这五个数中任取一个数，作为关于x的一元二次方程x²-x+k=0中的k值，则所得的方程中有两个不相等的实数根的概率是

查看试题解析
15. 如图，点A是反比例函数y= $\frac{K}{X}$ 的图象上的一点，过点A作AB⊥x轴，垂足为B，点C为y轴上的一点，连接AC、BC，若△ABC的面积为3，则k的值是．

查看试题解析
16. 如图，⊙O的半径为4，OA=8，AB切⊙O于B，弦BC∥OA，连接AC，则图中阴影部分的面积为．

查看试题解析
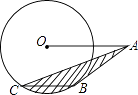17. 对于实数a，b，定义运算“⊗”： $a \otimes b {\begin{matrix} a b - b^{2} (a \geq b) \\ a^{2} - a b (a < b) \end{matrix}$ ，例如：5⊗3，因为5＞3，所以5⊗3=5×3﹣3²=6．若x₁ ， x₂是一元二次方程x²﹣6x+8=0的两个根，则x₁⊗x₂= ．

查看试题解析

三、解答题

18. 如图，直线y=x+m与反比例函数 $y = \frac{k}{x}$ 相交于点A（6，2），与x轴交于B点，点C在直线AB上且 $\frac{A B}{B C} = \frac{2}{3}$ ．过B、C分别作y轴的平行线交双曲线 $y = \frac{k}{x}$ 于D、E两点．

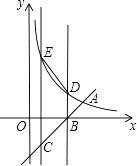(1)、求m、k的值；

(2)、求点D、E坐标．

查看试题解析
19. 阅读下面的材料：
解方程x⁴﹣7x²+12=0这是一个一元四次方程，根据该方程的特点，它的解法通常是：设x²=y，则x⁴=y² ， ∴原方程可化为：y²﹣7y+12=0，解得y₁=3，y₂=4，当y=3时，x²=3，x=± $\sqrt{3}$ ，当y=4时，x²=4，x=±2．∴原方程有四个根是：x₁= $\sqrt{3}$ ，x₂=﹣ $\sqrt{3}$ ，x₃=2，x₄=﹣2，以上方法叫换元法，达到了降次的目的，体现了数学的转化思想，运用上述方法解答下列问题．

(1)、解方程：（x²+x）²﹣5（x²+x）+4=0；

(2)、已知实数a，b满足（a²+b²）²﹣3（a²+b²）﹣10=0，试求a²+b²的值．

查看试题解析
20. 如图，⊙O的直径为10，在⊙O上位于直径AB的异侧有定点C和动点P，已知BC：CA=4：3，点P在半圆弧AB上运动（不与A、B两点重合），过点C作CP的垂线CD交PB的延长线于D点．

(1)、求证：AC•CD=PC•BC；

(2)、当点P运动到AB弧中点时，求CD的长．

查看试题解析
21. 如图，在一块正方形ABCD木板上要贴三种不同的墙纸，正方形EFCG部分贴A型墙纸，△ABE部分贴B型墙纸，其余部分贴C型墙纸．A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元．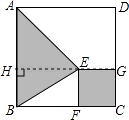

(1)、探究1：如果木板边长为1米，FC= $\frac{1}{2}$ 米，则一块木板用墙纸的费用需元；

(2)、探究2：如果木板边长为2米，正方形EFCG的边长为x米，一块木板需用墙纸的费用为y元，
①用含x的代数式表示y（写过程）．
②如果一块木板需用墙纸的费用为225元，求正方形EFCG的边长为多少米？

查看试题解析
22. 某数学兴趣小组开展了一次活动，过程如下：如图1，等腰直角△ABC中，AB=AC，∠BAC=90°，小敏将三角板中含45°角的顶点放在A上，斜边从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．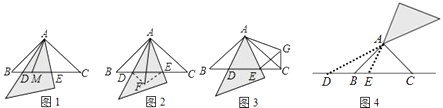

(1)、小敏在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠BAM，则AE也平分∠MAC．请你证明小敏发现的结论；

(2)、当0°＜α≤45°时，小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系：BD²+CE²=DE² ．同组的小颖和小亮随后想出了两种不同的方法进行解决：
小颖的想法：将△ABD沿AD所在的直线对折得到△ADF，连接EF（如图2）；
小亮的想法：将△ABD绕点A逆时针旋转90°得到△ACG，连接EG（如图3）；
请你从中任选一种方法进行证明．

(3)、小敏继续旋转三角板，请你继续研究：当135°＜α＜180°时（如图4），等量BD²+CE²=DE²是否仍然成立？请作出判断，不需要证明．

查看试题解析
23. 如图，在平面直角坐标系中，顶点为（2，﹣1）的抛物线交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，3），连接AB．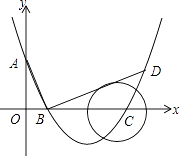

(1)、求此抛物线的解析式；

(2)、过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有怎样的位置关系，并给出证明；

(3)、已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积．

查看试题解析