湖北省黄冈地区2012届九年级四科联赛数学卷
试卷更新日期:2018-03-23 类型:竞赛测试
一、单选题
-
1. 已知三个关于x的一元二次方程ax2+bx+c=0,bx2+cx+a=0,cx2+ax+b=0恰有一个公共根,则
 的值为( ) A、0 B、1 C、2 D、32. 设a、b是整数,方程x2+ax+b=0的一根是 ,则 的值为( )
的值为( ) A、0 B、1 C、2 D、32. 设a、b是整数,方程x2+ax+b=0的一根是 ,则 的值为( )
A、2 B、0 C、-2 D、-13. 正实数a1,a2,….,a2011满足a1+a2+…..+a2011=1,设P= ,则( )A、p>2012 B、p=2012 C、p<2012 D、p与2012的大小关系不确定4. 如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )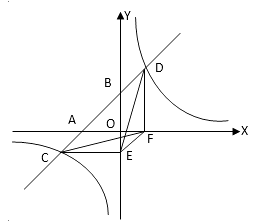 A、2 B、3 C、4 D、55. 如图,正方形ABCE的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,则△MAN的面积的最小值为( )
A、2 B、3 C、4 D、55. 如图,正方形ABCE的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,则△MAN的面积的最小值为( )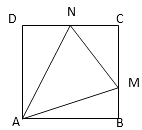 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
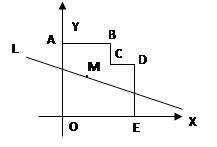
6. 已知实数x,y满足 ,则3x2-2y2+3x-3y-2012=7. 已知实数a,b,c满足a+b+c=10,且 ,则 的值是8. 如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0)、A(0,6)、B(4,6)、C(4,4)、D(6,4),E(6,0),若直线L经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线L的函数表达式是
 9. 如图,在正方形ABCD中,△AEF的顶点E,F分别在BC、CD边上,高AG与正方形的边长相等,连BD分别交AE、AF于点M、N,若EG=4,GF=6,BM= ,则MN的长为。
9. 如图,在正方形ABCD中,△AEF的顶点E,F分别在BC、CD边上,高AG与正方形的边长相等,连BD分别交AE、AF于点M、N,若EG=4,GF=6,BM= ,则MN的长为。 10. 的最小值为。
10. 的最小值为。
三、解答题
-
11. 边长为整数的直角三角形,若其两直角边边长是方程x2-(k+2)x+4k=0的两根,求k的值,并确定直角三角形三边之长。
12. 如图1,等腰Rt△CEF的斜边CE在正方形ABCD的边BC的延长线上,CF>BC,取线段AE的中点M 。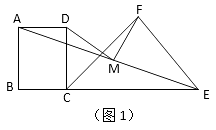 (1)、求证:MD=MF,MD⊥MF(2)、若Rt△CEF绕点C顺时针旋转任意角度(如图2),其他条件不变。(1)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由。
(1)、求证:MD=MF,MD⊥MF(2)、若Rt△CEF绕点C顺时针旋转任意角度(如图2),其他条件不变。(1)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由。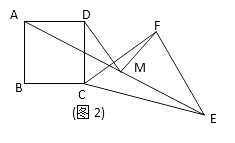 13. 黄冈市三运会期间,武穴黄商有一种姚明牌运动装每件的销售价y(元)与时间x(周)之间的函数关系式对应的点都在如图所示的图象上,该图象从左至右,依次是线段AB、线段BC、线段CD,而这种运动装每件的进价Z(元)与时间x(周)之间的函数关系式为Z=
13. 黄冈市三运会期间,武穴黄商有一种姚明牌运动装每件的销售价y(元)与时间x(周)之间的函数关系式对应的点都在如图所示的图象上,该图象从左至右,依次是线段AB、线段BC、线段CD,而这种运动装每件的进价Z(元)与时间x(周)之间的函数关系式为Z=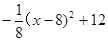 (1≤x≤16且x为整数)
(1≤x≤16且x为整数)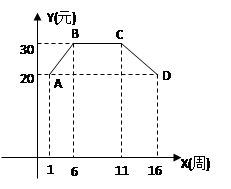 (1)、写出每件的销售价y(元)与时间x(周)之间的函数关系式;(2)、设每件运动装销售利润为w,写出w(元)与时间x(周)之间的函数关系式;(3)、求该运动装第几周出销时,每件运动装的销售利润最大?最大利润为多少?14. 如图,以O为原点的直角坐标系中,A点的坐标为(0,3),直线x=-3交x轴于点B,P为线段AB上一动点,作直线PC⊥PO,交于直线x=﹣3于点C。过P点作直线MN平行于x轴,交y轴于M,交直线x=﹣3于点N。
(1)、写出每件的销售价y(元)与时间x(周)之间的函数关系式;(2)、设每件运动装销售利润为w,写出w(元)与时间x(周)之间的函数关系式;(3)、求该运动装第几周出销时,每件运动装的销售利润最大?最大利润为多少?14. 如图,以O为原点的直角坐标系中,A点的坐标为(0,3),直线x=-3交x轴于点B,P为线段AB上一动点,作直线PC⊥PO,交于直线x=﹣3于点C。过P点作直线MN平行于x轴,交y轴于M,交直线x=﹣3于点N。 (1)、当点C在第二象限时,求证:△OPM≌△PCN;(2)、设AP长为m,以P、O、B、C为顶点的四边形的面积为S,请求出S与M之间的函数关系式,并写出自变量m的取值范围;(3)、当点P在线段AB上移动时,点C也随之在直线x=-3上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标,如果不可能,请说明理由。
(1)、当点C在第二象限时,求证:△OPM≌△PCN;(2)、设AP长为m,以P、O、B、C为顶点的四边形的面积为S,请求出S与M之间的函数关系式,并写出自变量m的取值范围;(3)、当点P在线段AB上移动时,点C也随之在直线x=-3上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标,如果不可能,请说明理由。