2011年全国初中数学竞赛试卷
试卷更新日期:2018-03-23 类型:竞赛测试
一、单选题
-
1. 设 ,则代数式 的值为( ).A、-6 B、24 C、 D、2. 在同一直角坐标系中,函数 ( )与 ( )的图象大致是( )A、
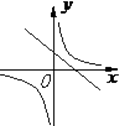 B、
B、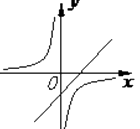 C、
C、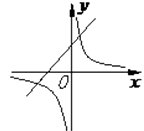 D、
D、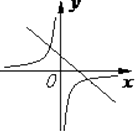 3. 在等边三角形ABC所在的平面内存在点P,使⊿PAB、⊿PBC、⊿PAC都是等腰三角形.请指出具有这种性质的点P的个数( )
3. 在等边三角形ABC所在的平面内存在点P,使⊿PAB、⊿PBC、⊿PAC都是等腰三角形.请指出具有这种性质的点P的个数( )
A、1 B、7 C、10 D、154. 若 , ,且满足 ,则 的值为( ).A、1 B、2 C、 D、5. 设 ,则 的整数部分等于( ).
A、4 B、5 C、6 D、7二、填空题
-
6. 若a是一个完全平方数,则比a大的最小完全平方数是。
7. 若关于 的方程 有三个根,且这三个根恰好可以作为一个三角形的三条边的长,则 的取值范围是.
8. 一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数字之和为奇数5的概率是.
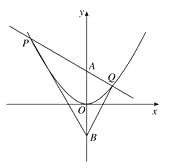
9. 如图,点 为直线 上的两点,过 两点分别作y轴的平行线交双曲线 ( )于 两点. 若 ,则 的值为.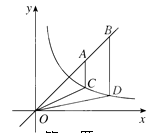 10. 如图,在Rt△ABC中,斜边AB的长为35,正方形CDEF内接于△ABC , 且其边长为12,则△ABC的周长为.
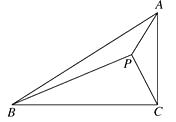
10. 如图,在Rt△ABC中,斜边AB的长为35,正方形CDEF内接于△ABC , 且其边长为12,则△ABC的周长为.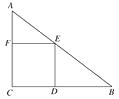
三、解答题