浙江省杭州市萧山区瓜沥片2016-2017学年八年级上学期四科联赛数学试卷
试卷更新日期:2018-03-23 类型:竞赛测试
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 2. 下列各图中,正确画出AC边上的高的是( )A、
2. 下列各图中,正确画出AC边上的高的是( )A、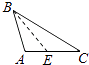 B、
B、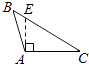 C、
C、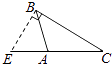 D、
D、 3. 若 成立,则下列不等式成立的是 ( )A、 B、 C、 D、4. 下列命题的逆命题不正确的是( )A、同角的余角相等 B、等腰三角形的两个底角相等 C、两直线平行,内错角相等 D、线段中垂线上的点到线段两端的距离相等5. 若点A( ,3)在y轴上,则点B( , )所在的象限是 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 正比例函数 的自变量取值增加2,函数值就相应减少2,则 的值为( )
3. 若 成立,则下列不等式成立的是 ( )A、 B、 C、 D、4. 下列命题的逆命题不正确的是( )A、同角的余角相等 B、等腰三角形的两个底角相等 C、两直线平行,内错角相等 D、线段中垂线上的点到线段两端的距离相等5. 若点A( ,3)在y轴上,则点B( , )所在的象限是 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 正比例函数 的自变量取值增加2,函数值就相应减少2,则 的值为( )
A、2 B、-2 C、-1 D、47. 如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )A、相等 B、互余 C、互补或相等 D、不相等8. 已知a>b>0,那么下列不等式组中无解的是( )A、 B、 C、 D、9. 如图,P为△ABC边BC上的一点,且PC=2PB,已知∠ABC=45°,∠APC=60°,那么∠ACB的度数是 ( ) A、45° B、75° C、90° D、60°10. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当PA=CQ时,连结PQ交AC边于D,则DE的长为 ( )
A、45° B、75° C、90° D、60°10. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当PA=CQ时,连结PQ交AC边于D,则DE的长为 ( )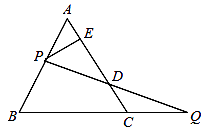 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 确定平面上一个点的位置,一般需要的数据个数为个.12. 函数 中自变量 的取值范围是.
13. 已知点P1(a,-3)和点P2(3,b)关于y轴对称,则a+b的值为.14. 如图,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于F,则∠CAF的度数是. 15. 如果不等式ax+b>0的解集是x>2,则不等式bx-a<0的解集是
15. 如果不等式ax+b>0的解集是x>2,则不等式bx-a<0的解集是
16. 如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 .
三、解答题
-
17. 解下列不等式(组)解下列不等式(组)
(1)、(2)、18. 如图,在Rt△ABC中,∠ACB=90°. (1)、用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(1)、用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)、连结AP,若AC=4,BC=8时,试求点P到AB边的距离.
19. 如图,点E在△ABC外部,点D在边BC上,DE交AC于点F.若∠1=∠2=∠3,AC=AE,求证△ABC≌△ADE.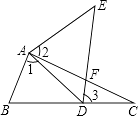 20. 如图,已知A(-3,-3),B(-2,-1),C(-1.-2)是坐标平面上三点.
20. 如图,已知A(-3,-3),B(-2,-1),C(-1.-2)是坐标平面上三点. (1)、写出点C关于y轴的对称点C’的坐标;(2)、画出将△ABC先向上平移5个单位,再向右平移3个单位后所对应的△A1B1C1.并写出△A1B1C1的各顶点坐标;(3)、将点C’向上平移 个单位后,点C’恰好落在△A1B1C1内,请你写出符合条件的一个整数 .(直接写出答案)
(1)、写出点C关于y轴的对称点C’的坐标;(2)、画出将△ABC先向上平移5个单位,再向右平移3个单位后所对应的△A1B1C1.并写出△A1B1C1的各顶点坐标;(3)、将点C’向上平移 个单位后,点C’恰好落在△A1B1C1内,请你写出符合条件的一个整数 .(直接写出答案)
21. 杭州市成功申办2022年亚运会,这将推动杭州市体育事业发展,为了促进全民健身活动的发展,某社区为辖区内学校购买一批篮球和足球,已知篮球和足球的单价分别为120元和90元.(1)、根据实际需要,社区决定购买篮球和足球共100个,其中篮球购买的数量不少于40个,社区可用于购买这批篮球和足球的资金最多为10260元,请问有几种购买方案;
(2)、若购买篮球 个,学校购买这批篮球和足球的总费用为 元,在(1)的条件下,求哪种方案能使 最小,并求出 的最小值.22. 阅读下列材料:解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1,即y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组 的解都为非负数.
(1)、求a的取值范围;(2)、已知2a﹣b=1,且,求a+b的取值范围;
(3)、已知a﹣b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示)
23. 如图1,在△OMN中,∠MON=90°,OM=6cm,∠OMN=30°.等边△ABC的顶点B与点O重合,BC在OM上,点A恰好在MN上. (1)、求等边△ABC的边长;(2)、如图2,将等边△ABC沿OM方向以1cm/s的速度平移,边AB、AC分别与MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移.设△ABC平移时间为t(s)
(1)、求等边△ABC的边长;(2)、如图2,将等边△ABC沿OM方向以1cm/s的速度平移,边AB、AC分别与MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移.设△ABC平移时间为t(s)①用含t的代数式表示AE的长,并写出t的取值范围;